Indexed In
- Genamics JournalSeek
- RefSeek
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Publons
- Euro Pub
- Google Scholar
Useful Links
Share This Page
Journal Flyer

Open Access Journals
- Agri and Aquaculture
- Biochemistry
- Bioinformatics & Systems Biology
- Business & Management
- Chemistry
- Clinical Sciences
- Engineering
- Food & Nutrition
- General Science
- Genetics & Molecular Biology
- Immunology & Microbiology
- Medical Sciences
- Neuroscience & Psychology
- Nursing & Health Care
- Pharmaceutical Sciences
Research Article - (2023) Volume 12, Issue 5
Chaos-Induced Self-Organized Criticality in Stock Market Volatility-An Application of Smart Topological Data Analysis
Carlos Pedro Gonçalves*Received: 26-Aug-2023, Manuscript No. SIEC-23-22746; Editor assigned: 28-Aug-2023, Pre QC No. SIEC-23-22746 (PQ); Reviewed: 11-Sep-2023, QC No. SIEC-23-22746; Revised: 19-Sep-2023, Manuscript No. SIEC-23-22746 (R); Published: 29-Sep-2023, DOI: 10.35248/2090-4908.23.12.331
Abstract
Smart Topological Data Analysis (STDA), previously employed to research the epidemiological dynamics associated with SARS-CoV-2, is applied to stock market sessions’ trading amplitudes for financial indexes and individual stocks, combining chaos theory, topological data analysis and machine learning. The methods employed uncover evidence of chaos-induced self-organized criticality in the daily trading amplitudes, used as a trading session’s volatility measure. The topological structure of the reconstructed attractors is researched upon, allowing us to characterize the dynamics of the underlying chaotic attractors and to link the main chaotic features to the markers of self-organized criticality, the implications of the research for finance, risk science and the complexity research are also addressed.
Keywords
Smart topological data analysis; Chaos theory; Financial volatility; Self-organized criticality; Chaosinduced self-organized criticality; Risk science
Introduction
Risk science takes risk as its object of research producing theories, methodologies and methods to address risk in any context, with the development of machine learning and data science methods, risk science’s research tools and modeling are undergoing a fundamental change in both their methodological basis and in the types of solutions that risk science can offer different decision makers when dealing with risk. From data-driven probability profiling [1] to the prediction of target risk variables [2,3], machine learning and Artificial Intelligence (AI) solutions can provide with effective ways to research and manage risk in different contexts.
In [2,3], chaos theory, topological data analysis and adaptive AI, comprised of an adaptive artificial agent were combined to predict key epidemiological risk variables linked to COVID-19, showing an application of the new methods of risk science employing Smart Topological Data Analysis (STDA), combining chaos theory, machine learning and topological data analysis.
In the present work, we extend and apply these same methods to the analysis and prediction of volatility risk in financial markets. The volatility risk is a major point of interest for both the financial industry community and the academia involved in researching financial markets, indeed, volatility risk expresses the threat associated with financial prices’ fluctuations with higher volatility being linked to higher price fluctuation risk exposure with consequences for financial management.
The major problem with volatility risk is that financial volatility is not fixed but, instead, shows evidence of a complex nonlinear dynamics with strong turbulence markers [4-9], which has led to the complexity sciences and the, related, econophysics communities research interest on financial volatility dynamics [4-14]. Models leading to complex nonlinear dynamics that produce financial turbulence have included agent-based models, autoregressive and stochastic volatility models, quantum-based models and chaos theory-based models, including multi-asset artificial financial markets modeled with globally coupled chaotic maps [6-14]. These models show sufficient conditions for the emergence of financial market turbulence and have played a key role in the construction of economic and financial theory.
On the empirical side, the research on financial market dynamics has showed power law signatures that typically occur in Self- Organized Criticality (SOC) dynamics [4-6,10,15,16] and chaotic markers [17-19], indicating the possibility of Chaos-Induced Self- Organized Criticality (CISOC), evidence that is in particular consistent with Chen’s empirical results on color chaos in the markets [17]. In [10], it was shown that coupled nonlinear chaotic maps could lead to SOC in the financial dynamics, which adds to the hypothesis of chaos as one possible source of financial SOC.
In the present work, we build on these empirical studies, addressing, for an exchange-traded fund, two financial indexes and three companies’ stocks, the volatility of each trading session, measured by the trading session’s price amplitude, that is, the difference between the maximum and minimum price in the trading session, the prediction of this variable’s dynamics is critical for both financial trading and financial risk management.
Applying methods from chaos theory and STDA [2,3], we find, in the daily trading sessions’ amplitudes, for the different series, markers of SOC and of chaos, including, in this last case, low dimensional attractors, positive largest Lyapunov exponents and topological regularities in the reconstructed attractors that can be exploited by topological adaptive AI systems for prediction with high coefficients of determination and low error.
We link the markers of SOC with the topological features of the attractor, with the evidence strongly supporting the hypothesis of CISOC.
The series analyzed, in the present work, include the SPY, which is an Exchange Traded Fund (ETF) on the S&P 500, the Russell 2000 and NASDAQ financial index series, which provide for the portfolio standpoint, and, for the company-level cases, we apply the methods to three aeronautical sector companies Lockheed Martin, Boeing and Airbus. The COVID-19 pandemic severely hit the aeronautical sector, however, our main findings show that all of the financial series exhibit evidence of a form of stochastic chaos characterized by low dimensional attractors, with positive largest Lyapunov exponents and a high level of predictability when employing an AI system equipped with topological adaptive learning, which learns to predict the target using the embedded phase points of the reconstructed attractor.
We analyze the dominant dimension in terms of permutation importance in the AI prediction and find that there is evidence of dynamical transitions between different dominant dimensions, transitions that follow Markov chain processes with near to maximum entropy equilibrium probabilities, extracted from the corresponding transition matrices, this evidence shows that the relation between the target signal and the reconstructed attractors does not decompose into a linear sum over the attractor’s degrees of freedom which comprise the different phase space dimensions, but, instead, the resulting nonlinear process should have nonlinear dependence upon some of the degrees of freedom, including the possibility of cross terms between different degrees of freedom such that the exploitable topological information associated with each dimension changes with time.
From an evolutionary computational standpoint, the emergent chaotic attractors’ exploitable topological signatures in signal prediction can be considered in terms of a computational symbolic dynamics with the symbol recorded at each step corresponding to the dimension with the maximum importance for the topological adaptive agent’s prediction of the target, the resulting computational dynamics is statistically characterized, as stated in the previous paragraph, by a Markov chain, with an equilibrium probability that is close to an equiprobable distribution over the different dimensions, which indicates that all dimensions are, in this case, relevant in predicting the target.
We also analyze the k-nearest neighbor graphs’ degree distribution and entropy measures, linking these last metrics to the major metrics associated with the reconstructed chaotic attractors and the markers of SOC.
The work is organized as follows: in section 2, we present the main concepts and methods, in section 3, we present the main results, and in section 4, we provide the conclusions, discussing the implications of the present work for both finance and risk science.
Main Concepts and Methods
Risk can be defined from its root in the Medieval Latin term resicum, which synthesized the concepts of periculum, with the meaning of peril, threat, and fortuna, with the meaning of fortune, luck, destiny and uncertainty, that is, one can speak of risk whenever one identifies threats, opportunities and there is an uncertainty in regards to the outcome, risk science, in turn, is concerned with fundamental and applied research on risk, with strong links to systems science and the complexity research [20], major lines of research that have an important bearing on risk science include the theory of SOC [10,15,16] and chaos [2,3,10,17-24].
The theory of SOC deals with the emergence of power law scaling in time and in event size in complex systems [10,15,16,24]. In the context of risk, which is a major line of applications of this theory, including examples such as earthquakes and financial turbulence [10,15,16,24], the occurrence of SOC in risk variables means that large events follow the same fractal order as the smaller events, which means that large catastrophes do not follow a separate dynamics from the system’s main dynamics, instead, they are produced by the system’s same dynamics that produces the smaller events.
Chaos theory, in turn, plays a major role in risk science, since it led to the distinction between the risk associated with external shocks that disrupt a system from without and the risk endogenously generated by the system’s own nonlinear dynamics [20].
Chaos, in deterministic nonlinear dynamical systems, corresponds to a family of dynamics that is characterized by bounded nonperiodicity with sensitive dependence upon initial conditions, characterized, in turn, by an exponential divergence of small deviations in initial conditions and random-looking spectral signatures upon signal analysis that are similar to those of a stochastic process, in this way, deterministic chaos can be characterized as a form of endogenous stochasticity in deterministic systems such that, even in the absence of noise, the dynamics will show random-like signatures and will have a fundamental unpredictability linked to the strength of the exponential divergence, measured by a positive maximum Lyapunov exponent [2,3,10,20-26].
While deterministic chaos characterizes closed systems with fixed dynamical equations, stochastic chaos is an open system’s dynamics that is characterized by a deterministic chaotic component and external noise terms that, in turn, can have different types of characteristics usually worked from within the theory of stochastic processes [2,3,10,22]. Stochastic chaos is a more complex type of stochastic process, since the deterministic component is chaotic and the feedback from the deterministic and noise components are processed in a complex nonlinear way by the system [2,3,10,22].
In nature, stochastic chaos is observable empirically in complex systems’ dynamics as the result of a self-organization that leads to an emergence of a noisy attractor, that is, even despite the noise (open system), the attractor’s dimensionality is stable and the markers of chaos, including positive Lyapunov exponents, can be identified [2,3,10,21,22].
In stochastic chaos, the strength of the noise is not sufficiently high to break the critical features of a chaotic attractor, namely, the positive largest Lyapunov exponent, the dimensionality resulting from the finite number of degrees of freedom associated with the deterministic component, the invariance of the attractor and the fact that the dynamics still follows an attractor with topological signatures of chaos despite the noise, keeping the main topological structure of chaos which can be exploited by adaptive AI systems equipped with topological learning units [2,3,10].
A relevant topological feature of a chaotic attractor is the existence of a skeleton of unstable periodic orbits, since the attractor is confined to a region in phase space, the system’s dynamics will recurrently track down a neighborhood of a periodic orbit for a while, until the exponential divergence associated with the chaotic dynamics sets in and the dynamics diverges from the periodic neighborhood, approaching the neighborhood of another unstable periodic orbit, this leaves markers of order in the chaotic dynamics in the form of recurrences that will exist in the overall nonperiodic dynamics, recurrences can also be explained, in the case of strange chaotic attractors, by the stretching and folding dynamics that leads to the fractal structure of the attractor [24-26].
In this sense, a chaotic dynamics can be characterized by its nonperiodicity, the fact that it is bounded, the sensitive dependence upon initial conditions and the pattern of recurrences [2,3,26], which is a key factor, since it is where Smart Topological Data Analysis (STDA) can be applied, in an empirical setting, for both the characterization of the chaotic dynamics and the prediction process, even without knowing the equations of motion associated with the chaotic attractor, STDA is also especially effective when dealing with stochastic chaos [2,3].
The methods of STDA were applied in [2,3] to the analysis and prediction of epidemiological series associated with SARS-CoV-2, in which a noisy chaotic dynamics near the onset of chaos was uncovered.
Considering a risk variable that follows a uni-dimensional time series, the first step in the application of chaotic time series analysis, using STDA, involves the choice of the embedding parameters for attractor reconstruction. Indeed, in accordance with Takens’ embedding theorem [25], given a sample time series x(t), t = 0,1,...,T −1, assuming that the series is generated from an attractor in a d-dimensional Euclidean phase space, the time series can be formally expressed as an observation function x(t) = g( p(t)) , where p(t) is a point in the d-dimensional Euclidean phase space. If p(t) is in an attractor, which is a dynamical invariant, then, the sequence p(t) is a trajectory in the attractor, and x(t) results from that trajectory [2,3,25,26]. In this case, p(t) can either be a flow (continuous time process) or the result of a map (discrete time-process).
When neither the equations of motion that may describe p(t)nor the observation function structure g are known, from Takens’ theorem, it follows that using an appropriate time delay and embedding dimension d, one can reconstruct an attractor’s orbit p(t)using d-dimensional tuples built from the time series x(t) , the method is based on using an appropriate time delay h and embedding dimension d in Euclidean space, the phase point is thus given by [2,3,25,26]:
p(t) = (x(t − (d −1)h),..., x(t − 2h), x(t − h), x(t)).............................(1)
From the reconstructed trajectory p(t), if the dynamics is in an attractor one can research the main attractor’s properties including recurrence structure, Lyapunov exponents and other topological features, employing topological data analysis, machine learning can also be applied here using topological features of the data for prediction, which is a key part of STDA, as shown in [2,3].
While different methods can be used for delay embedding, not all methods are generalizable, for instance, the use of false nearest neighbors for the dimension estimation only works if there is a stable attractor, when there are bifurcations with change of attractor stability, the dimensionality of the attractor can change, yet delay embedding can still be applied in prediction and bifurcation analysis, however, the false nearest neighbors method cannot be applied to the full series, as shown in [2].
An effective alternative method that provides good results even when bifurcations occur was proposed and used in [2] to deal with the bifurcation that occurred for the Oceania region in the number of new cases per million of COVID-19 confirmed infections and the new deaths per million from COVID-19, this same method was successfully applied to the analysis of the number of hospitalizations from COVID-19 in [3].
Given a set of alternative embedding dimensions, the method is based on choosing the embedding dimension that maximizes the predictability of the series using topological information, this involves employing an adaptive AI system that uses sliding window learning to predict the target series x(t) from an embedded point p(t −1) , and thus is capable of relearning, adapting to recurrence patterns, this AI system is equipped with a topological learning unit, either using k-nearest neighbors or a radius learner [2,3], and in this way is able to use the topological features of the data and adapt to these features in predicting the target.
Deploying this AI for different embedding dimensions, one can select the dimension that leads to the best results in terms of maximizing the coefficient of determination (R2), in this way, we are choosing, from a set of embedding dimensions, the dimension that leads to the maximum exploitable topological information in predicting the target, thus, we know that we have a good embedding in terms of capturing the topological order present in system’s dynamics [2,3], and can, from that embedding, apply topological data analysis methods to better characterize the system’s dynamics, the resulting embedded trajectory can, therefore, be used to analyze the corresponding dynamics. This adaptive topological AI-based method is effective both in dealing with bifurcations associated with changes in attractor stability, as shown in [2], as well as in cases of noisy attractors [2,3].
In the present article, the target risk variable is the daily trading amplitude, which, for a risky asset with price S(t) can be built from the daily trading session’s maximum Smax(t) and minimum Smin(t) prices, the target series is thus the daily volatility measured by the trading session’s amplitude:
v(t) = Smax(t) − Smin(t).............................................(2)
Now, given the time seriesv(t), t = 0,1,...,T −1. As a signal analysis method, we first apply rescaled range (R/S) analysis to characterize the memory pattern of the series estimating the Hurst exponent [6,24]. The Hurst exponent provides for a numeric characterization of the memory pattern of a time series. In the case of white noise, the exponent is equal to -0.5, while, for Brownian noise, it is equal to 0.5, a stronger persistent process is a black noise process which is characterized by a Hurst exponent greater than 0.5, this type of persistence often occurs in risk dynamics like natural disasters [24], it was also identified in the COVID-19’s epidemiological data, from spectral analysis [2,3].
The estimation of the Hurst exponent involves dividing a time series into non-overlapping intervals of length S, and, then, for each subseries of length s estimating the respective range and the standard deviation, calculating the mean of the quotients of the calculated ranges by the respective standard deviations, this calculation is repeated for different sizes S and then the Hurst exponent is extracted by fitting a straight line for the log-log plot of the calculated means and sizes, the log-log straight line is evidence of a power law scaling in the temporal dependence of the data [24].
A major characteristic of financial volatility is long memory with slow decaying autocorrelation functions, which means that we are not dealing with white noise processes, a point that also excludes white chaos as an underlying process, that is, chaos with a white noise spectrum. While white chaos has a white noise spectrum, chaos with a power law scaling in the rescaled range analysis is more complex, it can range from differentiable flows to chaotic maps that show turbulence markers in generated series that are close to power-law noises and Chaos-Induced Self-Organized Criticality (CISOC) [2,3,10,17,27].
As previously stated, SOC is characteristic of a wide range of risk dynamics, there are two main features of SOC. One feature is temporal scaling associated with long- memory processes. In the case of different risk problems, such as those related to natural disasters and other risk variables these often show a Hurst exponent greater than 0.5, which is characteristic of persistent noises (black noises) [2,3,24]. The second feature of SOC is scale invariance in the probability distribution, a feature that also occurs in different risk variables including earthquakes [15,16,24]. Chaos, as stated, is one possible source of these features [2,3,10,17,26,27], in [10] a financial model based on coupled chaotic maps was already capable of generating both of these features, constituting an example of CISOC.
To identify a possible presence of SOC in the daily financial amplitudes we apply not only the R/S analysis to estimate the Hurst exponent for each series, but we also perform a histogram analysis, following [15,16], and plot the histogram in a log-log scale, fitting a linear regression line, if a linear scaling is present, this indicates a level of scale invariance in the size of the market volatility events, that is, a fractal law associated with the event size distribution [10,15,16].
After analyzing the markers of SOC, we apply the delay embedding method for attractor reconstruction, in order to evaluate the hypothesis of CISOC. The first step is the choice of the embedding lag. There is no unique general method for choosing the embedding lag, the first zero crossing of the autocorrelation function is a possible method, however, in the case of color chaos, that is, chaos that does not have a white noise spectrum and that shows long memory with power law decaying autocorrelations, which occurs for persistent processes, and more strongly so in chaotic dynamics with strong persistence, that is, chaos leading to signals with Hurst exponents higher than 0.5, we find that the first zero crossing of the autocorrelation function can sometimes lead too long lags for embedding, since the autocorrelation function is slow decaying due to the persistent signal [2,3].
The possibility of using the first zero crossing of the partial autocorrelation function provides, in these cases, for a better solution than the first zero crossing of the autocorrelation function. The other possibility would be the use of the mutual information function, as introduced in [28], however, and again, in series with strong persistence, this method may also lead to an embedding that produces a squeezing of the attractor around a diagonal in phase space, this is the case for instance in the COVID-19 epidemiological data worked in [2] which had black noise spectra, after initial tests with the mutual information, the squeezing effect led us to work with the quarantine period instead of the mutual information which led to better results.
In the present work, we also identified Hurst exponents greater than 0.5, in this case, we found good results from using the first zero crossing of the partial autocorrelation function to select the lag. The partial autocorrelation also decays, in our analyzed series, with a power law scaling, which is another indicator of SOC, but does not lead to too long lags for embedding, since the first zero crossing occurs sooner than that of the autocorrelation function.
Now, for the dimension estimation, we work, as previously stated, with a similar method to the one used in [2] to deal with a bifurcation and in [3] for the US and Canada’s hospitalizations from COVID-19, in which a machine learning algorithm, using topological adaptive learning, was used to identify the embedding dimension, from a range of alternative dimensions, for which the best performance in target prediction could be obtained, in this way, from a range of alternative dimensions one would select the dimension for which the maximum exploitable topological information could be extracted by an adaptive topological learner [2,3].
In this method, one uses a nearest neighbors’ machine learning algorithm that exploits topological information, either a radius learner or a k-nearest neighbors’ learner, in the present work, we will be using the k-nearest neighbors’ algorithm, which will support the subsequent topological data analyses.
The method involves deploying an adaptive AI system that uses the topological regularities in the embedded trajectory to predict the target series, using a sliding window of sizewfor relearning, in order to perform the single period prediction for the next period’s trading amplitude v(t +1) , that is, the agent forms the following conditional expectation:
E[v(t +1) | p(t),w, k] = f ( p(t),w, k,t)............................(3)
where we denoted by E[v(t +1) | w, k] the prediction for v(t +1) conditional on the phase point p(t) , on the window learning size w and on the number of nearest neighbors k. The AI is trained using the feature set of embedded points {p(t − w−1),..., p(t −1)}and target variable values {v(t − w),...,v(t)}. In this way, the AI learns to predict the next value of the target using the previous value of the embedded phase point, which means that the prediction function on the right of equation (3) may change with time t. The relearning allows the AI to adapt to attractor epochs making the method especially robust in the case of turbulent and noisy series, which is effective when dealing with open systems and stochastic chaos [2,3].
Following [2,3], given a set of dimensions d0 d1.... dN we identify which dimension leads to the best prediction performance of the target series, using the R2 score as a performance metric for selecting the dimension, this dimension corresponds to the embedding dimension for which the adaptive topological learner is able to extract the most information from the topological structure of the embedded trajectory in order to predict the target series [3], which means that, from the set of alternative embeddings, we use an embedding where the most topological order is captured, this embedding can then be used to apply topological data analysis and nonlinear dynamical analysis methods in order to characterize the attractor.
The R2 score also provides for an indicator of the degree to which the topological features of the attractor allow for the prediction of the target series’ next value, providing, also, with an approximation to the level of noise present in the data.
For the number of k nearest neighbors, the value should be selected as not too low, nor too high, in the present work we set it to 40% of the learning window size. The learning window also needs to be considered, in this case, too long windows can lead to a smoothing of the predictions, too short windows are insufficient for learning. In the present case, we use a 10-day window for learning, which corresponds 10 trading days, equivalent to two trading weeks.
After having obtained an embedding using the above method, we employ Eckmann et al. method for the Lyapunov spectrum estimation [2,29]. This method allows one to estimate the spectrum of Lyapunov exponents for a multidimensional attractor. The method allows one to set a matrix dimension dM and study the behavior of the exponents for increasing embedding dimensions d with d not smaller than dM , we set the matrix dimension to the embedding dimension extracted from the adaptive topological AI method described above. The presence of positive exponents is evidence favorable to chaos, namely, if we find a convergence of the Lyapunov spectrum as the embedding dimension increases and some of the exponents converge to positive values, then, this is evidence favorable to a chaotic attractor.
We expect that, dealing with dissipative chaos, the sum of the exponents will be negative, so we will have positive and negative exponents. Besides the Lyapunov exponents, we also address the topological structure of the attractor applying a k-nearest neighbors’ analysis based on three parts.
The first part of the k-nearest neighbors’ topological analysis is the predictability analysis, where, using the previously obtained delay embedding parameters, we evaluate the performance of the adaptive agent for different values of k in a range of values. This allows us to calibrate the value of k, within the range, that leads to the best prediction performance, this is the number of neighbors that maximize the exploitable information by an adaptive topological learner.
We begin by calculating, for different values of k, the R2 from the adaptive learner, using the previously obtained embedding dimension and lag, and use this to analyze the pattern of predictability for a range of values of k-nearest neighbors, this, in turn, provides us not only with an analysis for the topological predictability of the system’s dynamics for different number of nearest neighbors but also provides us with a way to calibrate the subsequent topological analyses which will require a selection of the k parameter for further analyses of the attractor’s topological profile [2,3].
After selecting the value of k that leads to the highest predictability, we begin by reporting statistics that characterize the degree of predictability of the target series from the attractor, namely, the correlation coefficient of the adaptive AI’s predictions and the target values, the Root Mean Squared Error (RMSE) divided by the series’ amplitude, which provides for a relative estimate of the size of the RMSE given the data amplitude, and the R2 itself [2,3].
Secondly, for each of the best values of k, we obtain the permutation importance of each feature in the training data, scored by the R2 score, the permutation importance is a machine learning method that can be generally applied allowing one to calculate each feature’s importance [30]. In this case, each feature corresponds to each phase space dimension, thus, for each training set of the best performing adaptive topological learner, in each sliding window (re)learning instance, we calculate the effect on R2 from permuting each dimension, the AI system’s reliance on each dimension for prediction will be determined in terms of the way in which its prediction is affected by changing the order of the dimensions.
If a specific dimension is more important than the others in the prediction of the target, then, it is a dominant dimension being used by the AI in the prediction of the target. Thus, for instance, if a dynamics is characterized by an autoregressive linear combination of the embedding tuple, with no nonlinear dependences, then, with each relearning, the order of importance of the dimensions will be fixed, and the dimensions’ importance will not change significantly. Also, even if we do not have an autoregressive linear combination associated with the embedding process, a given dimension may be stably more impactful than the others, in which case, the dominant dimension will also be dynamically stable.
By contrast, chaotic systems with multiple degrees of freedom may be characterized by nonlinear functions of the degrees of freedom, including possibly cross-products of the different degrees of freedom which means that the importance of each phase space dimension in the system’s dynamics for the prediction of the target is expected to change with time, depending on the trajectory in the attractor. This means that the sliding window relearning process will lead to changes in the dominant dimension, which in turn provides for the basis of a symbolic computational analysis directed at the dominant dimension. In this case, we apply the following method:
• Step 1: We extract the dominant dimension for each relearning step of the topological learner obtaining a time series given by the symbolic sequence of dominant dimensions, using the permutation importance ordering of the dimensions;
• Step 2: We divide the symbolic sequence in two halves (two subsamples) and calculate the transition matrix for each subsample and, also, for the full sample;
• Step 3: We extract the stationary Markov equilibrium distribution from the full sample transition matrix and each subsample’s transition matrices;
• Step 4: We apply the chi-square test in order to test whether each subsample’s equilibrium distribution is equal to the full sample’s equilibrium distribution.
If, at the end of step 4, the null hypothesis of the chi-square test is not rejected, then, we have evidence favorable to the stationarity of the equilibrium distribution extracted from the transition matrix, in which case, we can analyze the equilibrium distribution for the transition between dominant dimensions, which allows us to identify the dynamical computational pattern associated with the dominant dimension (symbolic) dynamics in target prediction for the adaptive topological learner.
When the chi-square test’s null hypothesis is not rejected and the equilibrium distribution has a high probability associated with a specific dimension, then, this is evidence that there is a specific dominant degree of freedom, and, in that case, we need to consider the possibility of an autoregressive model with that dimension as a regressor and then add progressively the remaining dimensions and evaluate the statistics for the autoregressive process performance in prediction.
When the chi-square test’s null hypothesis is rejected or the equilibrium distribution does not have a dimension standing out with a probability higher than the others, then, we find that there is a variability in the change of dominant dimension in prediction which is evidence favorable to a dynamics that features nonlinear dependences including possible cross-products of degrees of freedom, which may occur for a multidimensional chaotic attractor.
In order to better characterize the Markov equilibrium distribution, when the chi-square test’s null hypothesis is not rejected, we calculate the Shannon entropy of the distribution and compare it to the maximum entropy, the closer the distribution is to the maximum entropy, the greater the evidence of dimension importance change corresponding to nonlinearities or cross-products of degrees of freedom that may change, in terms of evolutionary computational dynamics, the importance of each dimension in the prediction of the target.
These analyses are directed at the predictability of the target series and the dimensions’ importance, which not only provides for an evaluation of the possible performance of an adaptive AI system that can be deployed for risk management but also allows one to characterize the type of dynamics and the degree to which the reconstructed attractor contains information relevant for the prediction of the target, including the relevance of each degree of freedom corresponding to a different phase space dimension.
The third part of the k-nearest neighbors’ topological analysis is the k-nearest neighbors’ graph analysis. This is an undirected graph for which the vertices correspond to each phase point and the edges connect each phase point to its k-nearest neighbors. This graph provides for another representation of the topological structure of an attractor’s recurrences. In this case, we use the value of k that leads to the highest coefficient of determination, obtained in the first part of the k-nearest neighbors’ topological analysis, in this way, we can analyze the complexity of the recurrence evaluated in terms of the number of k neighbors for the best performing topological learner in the prediction of the target.
To characterize the complexity of the k-nearest neighbors’ graph we analyze the degree distribution and calculate two entropy measures, namely, the relative degree entropy [2], which ranges from 0 to 1, where 0 corresponds to the case where each node has the same degree and 1 to the case where we get an equiprobable distribution over the degree values for a randomly selected degree [2].
A second entropy measure that we calculate is the Kolmogorov- Sinai (K-S) entropy for the graph [2], which provides for relevant information on the recurrence structure. Indeed, considering the adjacency matrix, we obtain a topological binary transition matrix from each phase point to each of its k-nearest neighbors. Considering a random walker that follows the nearest neighbor adjacency, the K-S entropy is the dynamical entropy of the Markov process on the k-nearest neighbors’ graph, in this sense, it provides for a measure of the rate at which information is generated by the graph of k-nearest neighbors’ adjacencies, providing for a measure of the topological complexity of the attractor’s recurrences addressed in terms of the graph’s adjacency matrix [2]. We then perform an analysis of the relation between the two entropy measures and previously calculated major statistics such as the R2 (predictability performance), largest Lyapunov exponents and Hurst exponents, as well as fractal scaling in the signal distribution.
Results and Discussion
The dataset was obtained from Yahoo Finance and is comprised of the daily series of trading sessions’ amplitudes calculated using equation (1), for the Exchange Traded Fund (ETF) SPY, which is an ETF that is aimed to track the financial index S&P 500, for the NASDAQ, which covers the technological sector and for the Russell 2000 index, which covers small caps. The individual companies for which the daily trading session amplitudes were calculated are Lockheed Martin, Boeing and Airbus, below are the periods covered for each series along with the stock market identifier (“tick”) inside brackets:
• SPY (SPY)-from 29-01-1993 to 08-05-2023, size: 7623 daily observations.
• NASDAQ (^IXIC)-from 12-12-1984 to 08-05-2023, size 9678 daily observations.
• Russell 2000 (^RUT)-from 10-09-1987 to 08-05-2023, size 8986 daily observations.
• Lockheed Martin (LMT)-from 03-01-1977 to 08-05-2023, 11687 daily observations.
• Boeing (BA)-from 02-01-1962 to 08-05-2023, 15443 daily observations.
• Airbus (AIR.PA)-from 03-09-2001 to 08-05-2023, 5567 daily observations.
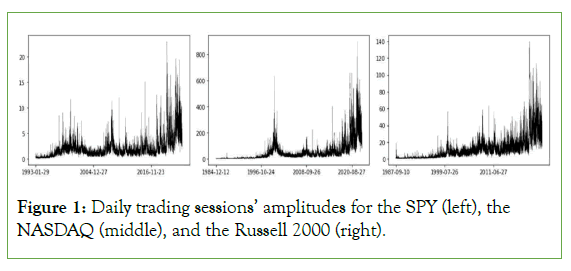
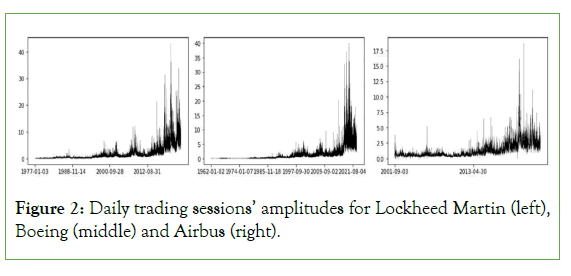
In Figure 1, we show the time series charts for the daily trading sessions’ amplitudes obtained for the SPY (left), the NASDAQ (middle) and the Russell 2000 (right), in Figure 2, we show the time series charts for the daily trading sessions’ amplitudes obtained for Lockheed Martin (left), Boeing (middle) and Airbus (right). The markers of turbulence, including large jumps, volatility buildups and clustering, can be seen in each of the series, which reinforces the evidence of turbulence in financial volatility both at the single company level and at the level of the ETF and the two stock market indexes.
Figure 1: Daily trading sessions’ amplitudes for the SPY (left), the NASDAQ (middle), and the Russell 2000 (right).
Figure 2: Daily trading sessions’ amplitudes for Lockheed Martin (left), Boeing (middle) and Airbus (right).
As shown in Table 1, all series exhibit evidence of long range dependence, with Hurst exponents all higher than 0.75, with the strongest persistence found for the SPY, Lockheed Martin and Boeing, all with Hurst exponents above 0.85, these are followed by the Russell 2000 and NASDAQ indexes, which have Hurst exponents lower than 0.85 but higher than 0.83, finally, Airbus shows the lowest signal persistence, with a Hurst exponent of 0.7512. In all cases, the long-range dependence is consistent with SOC.
| Hurst exponent | Lag | |
|---|---|---|
| SPY | 0.8564 | 15 |
| NASDAQ | 0.831 | 15 |
| Russell 2000 | 0.8392 | 19 |
| Lockheed Martin | 0.8522 | 17 |
| Boeing | 0.8503 | 17 |
| Airbus | 0.7512 | 14 |
Table 1: Hurst exponents estimated from R/S analysis and first lag with a zero crossing of the partial autocorrelation function.
In terms of embedding lag selection, the Russell 2000 has the longest period for the zero crossing of the partial autocorrelation function, in this case, 19 days, followed by the Lockheed Martin and Boeing series which have the first zero crossing at lag 17, next comes the SPY and the NASDAQ, which have the first zero crossing at lag 15 and, finally, comes the Airbus series, with the lowest first zero crossing of the partial autocorrelation function, which occurs at lag 14.
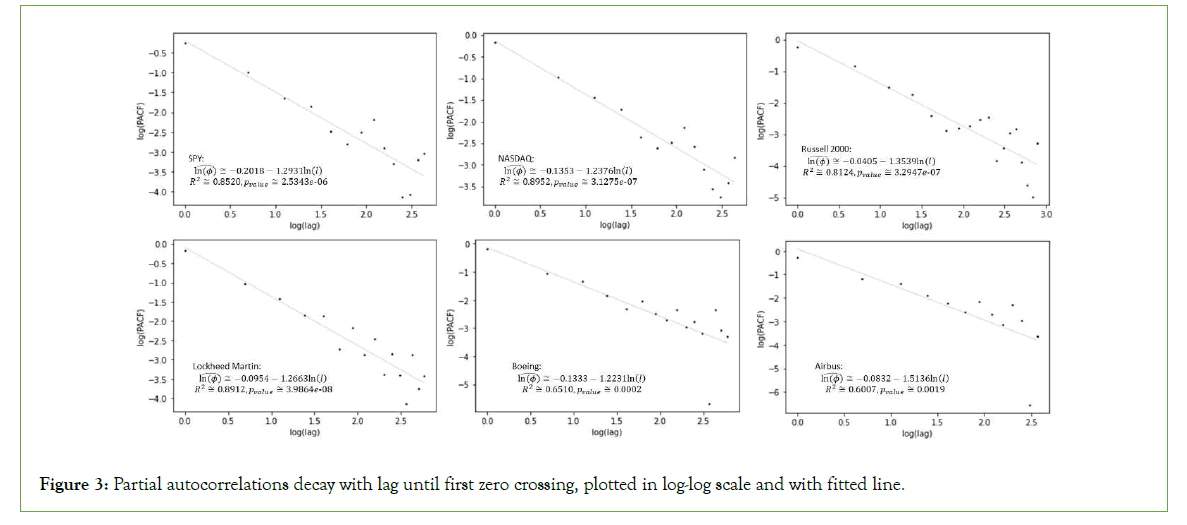
While the Hurst exponent indicates very slow decaying autocorrelations, if we consider the partial autocorrelations’ decay we not only get long lags for the first zero crossing but also a power law decay in the partial autocorrelations, with slopes ranging between -1.5 and -1.3, (-1.293 for the SPY, -1.2376 for the NASDAQ, -1.3539 for the Russell 2000, -1.2663 for Lockheed Martin, -1.2231 for Boeing and -1.5136 for Airbus) as shown in Figure 3, which reinforces the strong persistence of the process consistent with SOC. This evidence means that market volatility will tend to cluster for a long time, which is typical of a turbulent dynamics with periods of lower volatility clustering together and then periods of high volatility also clustering together.
Figure 3: Partial autocorrelations decay with lag until first zero crossing, plotted in log-log scale and with fitted line.
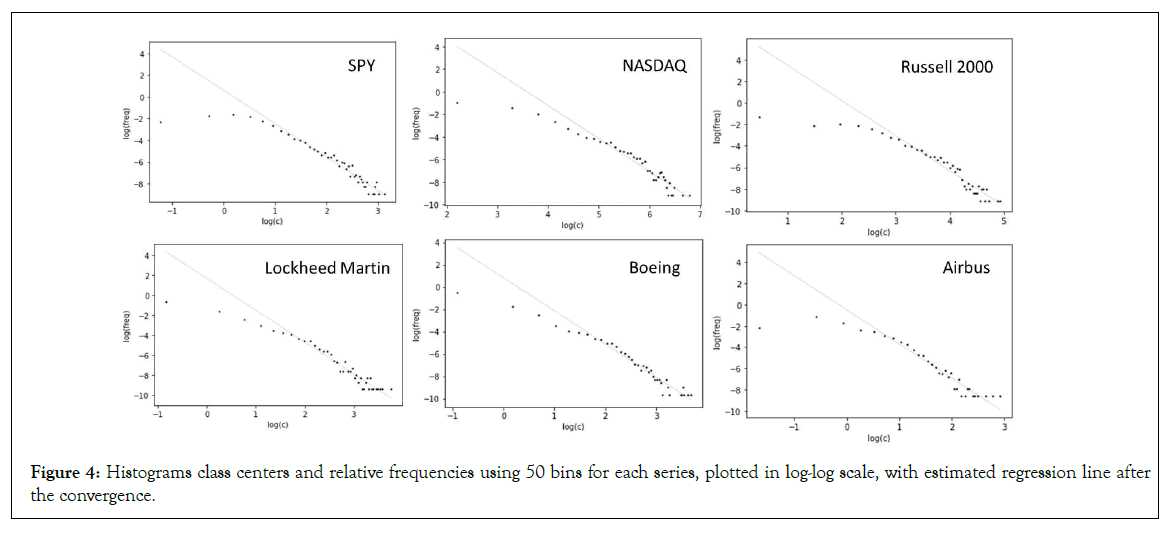
The power law decay in temporal dependence is, as stated, indicative of SOC. A second marker of SOC is found from the analysis of the histogram for each series, as shown in Table 2 and Figure 4. We find that each histogram has a convergence to power law decay.
|
Slope |
R2 |
p-value | |
|---|---|---|---|
| SPY | -3.0683 | 0.9572 | 0 |
| Nasdaq | -2.9142 | 0.9286 | 0 |
| Russel 2000 | -3.2618 | 0.943 | 0 |
| Lockheed Martin | -3.1816 | 0.9435 | 0 |
| Boeing | -2.9665 | 0.9567 | 0 |
| Airbus | -3.2171 | 0.9264 | 0 |
Table 2: Estimated slopes from figure 4, along with regression R2 and p-values associated with each slope.
Figure 4: Histograms class centers and relative frequencies using 50 bins for each series, plotted in log-log scale, with estimated regression line after the convergence.
There are two features that allow us to characterize the distribution, first, in the convergence to the power law, the lower values have a lower frequency than expected from the power law which means that there are laminar periods in the daily trading sessions’ amplitudes’ dynamics, however, these periods have a lower probability than they would have under the power law scaling. The second feature, is the power law itself, after the fifth class in the histogram, the dynamics follows the power law scaling with high R2 values for the fitted regression, all above 90%.
The regression was estimated on the power law decaying region, which is the dominant region of the distribution. This region indicates that the turbulence has a fractal scaling in its distribution, with the fractal dimensions equal to the symmetric of the slope estimated in Table 2 and Figure 4, which means that there is a statistical scale invariance associated with the frequencies of events, with the same process responsible for the large events (large jumps) being responsible for the lower jumps, apart from the lower laminar periods before the convergence to the power law.
A relevant point of the fractal scaling in the dominant power law region is that the fractal dimension, corresponding to the symmetric of the slope, is, in each case, close to 3 and statistically significant, the fact that the values are all close to each other for different series and lengths, lends a high consistency to the distribution structure.
These features, along with the long-range power law dependence both in the Hurst exponent and in the decay of the partial autocorrelations provides strong evidence of SOC in the financial series.
Now, the main point is the source of SOC, more specifically the possibility of it being induced by a chaotic process (CISOC), as discussed in the previous section. To investigate this possibility, we perform multiple delay embeddings setting the first zero crossing of the partial autocorrelation function and varying the embedding dimensions from 2 to 15. Then we employ an adaptive topological learner to predict the daily amplitude series using the reconstructed attractor, with a 10 trading day sliding learning window and a k-nearest neighbors’ learning unit, setting k to 4, which represents 40% of the size of the training window.
In Table 3, we report the dimension with the best performance of the k-nearest neighbors’ adaptive learner, measured by the coefficient of determination.
| Dimension | R2 | |
|---|---|---|
| SPY | 5 | 58.77% |
| NASDAQ | 8 | 72.68% |
| Russell 2000 | 6 | 67.19% |
| Lockheed Martin | 2 | 71.57% |
| Boeing | 8 | 73.15% |
| Airbus | 2 | 57.51% |
Table 3: Optimal embedding dimensions and corresponding adaptive agent’s R2, selected from a set of dimensions from 2 to 15, for an adaptive artificial agent with 10 trading days sliding learning window and a k-nearest neighbors’ learning unit, setting k to 4 and using a Euclidean metric.
We find, in each case, an overall high level of topological predictability of the series with good performance by the adaptive agent, the best prediction performance is obtained for an eightdimensional embedding in the case of the NASDAQ and Boeing with an R2 of 72.68% and 73.15%, respectively.
In the case of Lockheed Martin and Airbus, the optimal embedding dimension is 2, with an R2 71.57% and 57.51%, respectively. For the Russell 2000, the optimal embedding is six-dimensional, with an R2 of 67.19%, for the SPY the optimal embedding is fivedimensional with an R2 of 58.77%.
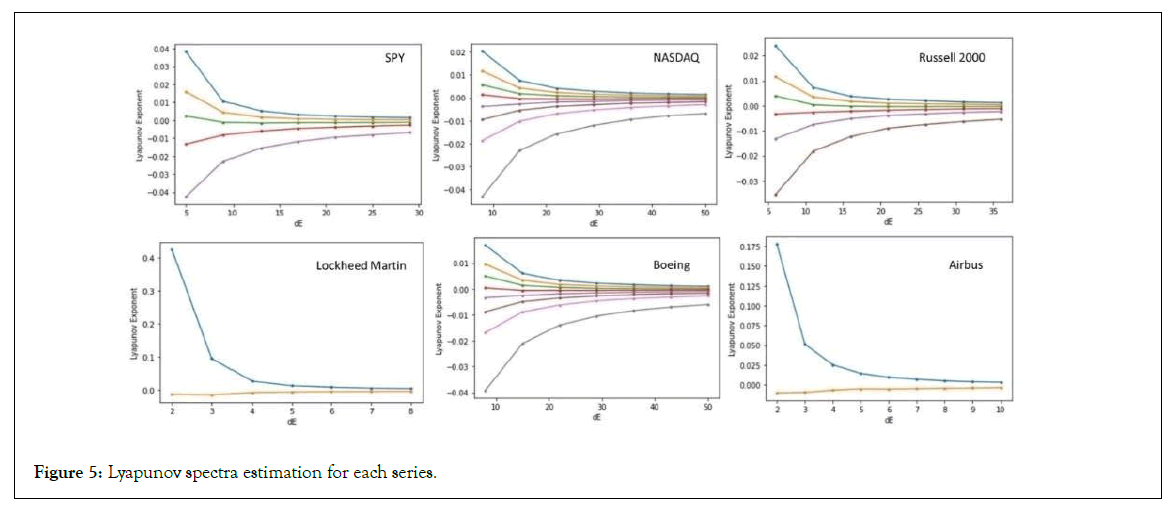
The resulting optimal dimensions vary considerably, indicating that different financial series can have different attractor dimensionalities, but they are all low dimensions. Now, using these embedding dimensions we estimated the Lyapunov spectrum for each series, as shown in Table 4 and Figure 5.
| Lyapunov exponents | SPY | NASDAQ | Russell 2000 | Lockheed Martin | Boeing | Airbus |
|---|---|---|---|---|---|---|
| L1 | 0.00143 | 0.00145 | 0.00119 | 0.00401 | 0.00106 | 0.00297 |
| L2 | 0.00024 | 0.00076 | 0.00038 | -0.00401 | 0.00048 | -0.0037 |
| L3 | -0.00114 | 0.00016 | -0.00037 | 0.00002 | ||
| L4 | -0.00271 | -0.00039 | -0.00114 | -0.0004 | ||
| L5 | -0.00677 | -0.00093 | -0.00231 | -0.00097 | ||
| L6 | -0.00177 | -0.00544 | -0.00162 | |||
| L7 | -0.00297 | -0.00265 | ||||
| L8 | -0.00685 | -0.00599 |
Table 4: Estimated Lyapunov spectra for each series at the end of the convergence.
Figure 5: Lyapunov spectra estimation for each series.
As can be seen in Figure 5, there is a convergence for all series, in Table 4, we show the estimated spectrum, the largest exponent is always positive, which, along with the high predictability results obtained from the embedding, indicating a strong deterministic signal but with some noise, is evidence favorable to a stochastic chaotic dynamics associated with each attractor.
In the case of the attractors with dimensions higher than 2, we find that the largest Lyapunov exponents are close to each other in terms of value, however, there is a division between the SPY and the NASDAQ, both with a largest Lyapunov exponent slightly higher than 0.0014, and then we have Boeing and the Russell 2000 with Lyapunov exponents close to 0.0011. In the case of the twodimensional attractors we get a convergence to a higher value of the largest Lyapunov exponent, in the case of Lockheed Martin to 0.00401 and in the case of Airbus to 0.00297.
For the higher dimensional attractors, we find that the SPY and Russell 2000 both have two positive Lyapunov exponents with the remaining exponents being all negative. For the NASDAQ and Boeing we get three positive Lyapunov exponents, with the third having a value close to zero, 0.00016, in the case of NASDAQ, and 0.00002, in the case of Boeing. The sum of the Lyapunov spectra is negative for all attractors, however, in the case of the two-dimensional attractors it is close to zero, indeed, for Lockheed Martin the spectrum sum is around -0.00001 while for Airbus it is around -0.00073. The positive but low values of the largest Lyapunov exponents can be explained by the strong persistence and power law decay in correlations.
For all series, the high predictability with some noise, the Lyapunov spectrum convergence and positive Lyapunov exponents with a negative spectra sum constitute evidence consistent with a form of stochastic chaos with noise resilient low-dimensional attractors underlying the daily trading sessions’ amplitudes, which are characterized by power law scaling in the temporal correlations and in the statistical distribution, in this sense there is evidence favorable to CISOC.
Now, if we calculate the correlation between the Hurst exponent and the zero crossing lag, we obtain a positive intermediate correlation of around 0.5498, which means that the series that have a higher Hurst exponent also tend to have a later zero crossing of the partial autocorrelation function, however, other factors enter into play, in this case, the exponential divergence of nearby trajectories associated with largest positive Lyapunov exponents as we just saw, this is a characteristic of power law chaos, or color chaos [17], which characterizes CISOC [2,3,10,27]. In CISOC, the power law decay in correlations leads to a long-range dependence and, thus, to a stronger mirroring of neighboring cycles, which leaves a marker in the recurrence structure, on the other hand, the positive largest Lyapunov exponent, which tends to be low, characterizes an exponential divergence of nearby trajectories.
The correlation between the largest Lyapunov exponents and the Hurst exponents is, in this case, negative and approximately equal to -0.3103, which is a weak correlation. A stronger negative correlation is obtained between the largest Lyapunov exponent and the corresponding attractor dimensionality, in this case, the correlation is negative and, to a four decimal places’ approximation, equal to -0.8773.
Considering the fractal dimensions associated with the power law decay in the statistical distribution of trading amplitudes’ fluctuations, which are the symmetric of Table 2’s slopes, we find that there is a positive correlation of approximately 0.4638 between the largest Lyapunov exponent for each series and that dimension.
In terms of the relation between these fractal dimensions and the underlying attractor dimensionality, we find a strong negative correlation of around -0.7267 between the attractor dimensionality and these fractal dimensions, which means that the higher the dimensionality of the attractor, the lower tends to be the fractal dimension associated with the statistical distribution’s power law decay. The correlation with the Hurst exponent and the attractor dimensionality is positive but weaker, approximately 0.4498.
These results effectively link the main chaotic metrics of the reconstructed attractors (largest Lyapunov exponent and the estimated attractor dimensionality) with the main SOC metrics.
Considering, now, the prediction performance, using the previously obtained embedding parameters, we find, as reported in Table 5, that the adaptive AI’s performance, measured in terms of the R2 metric, increases with the number of k nearest neighbors, for the number k varying from 2 to 6. For all financial series, the best prediction performance is obtained for 6 nearest neighbors, except for Boeing, where the best prediction performance is obtained for 5 nearest neighbors.
| 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|
| SPY | 54.06% | 57.11% | 58.77% | 59.60% | 60.34% |
| NASDAQ | 67.86% | 70.70% | 72.68% | 73.06% | 73.63% |
| Russell 2000 | 61.28% | 65.16% | 67.19% | 67.97% | 68.53% |
| Lockheed Martin | 65.25% | 69.60% | 71.57% | 72.68% | 73.06% |
| Boeing | 67.03% | 70.57% | 73.15% | 73.95% | 73.72% |
| Airbus | 48.68% | 54.20% | 57.51% | 58.15% | 58.82% |
Table 5: R2 prediction score of the adaptive AI as a function of the number of k nearest neighbors used in prediction with k varying from 2 to 6, using a sliding learning window of 10 trading days.
As shown in Table 5, for the NASDAQ, Lockheed Martin and Boeing we get a prediction performance, for the best performer, that exceeds the 73% R2 score, followed by the Russell 2000, for which the adaptive topological learner gets a score of 68.53%, then comes the SPY with a score of 60.34% and finally Airbus with a score of 58.82%. In this way, the AI is capable of capturing more topological information with the increase in the number of nearest neighbors, reducing the prediction error. These results reinforce the argument that the underlying attractor has exploitable topological information for the prediction of the target series, reinforcing the hypothesis of noise-resilient chaos leading to both low dimension attractors and to noise-resilient topological patterns.
These results are reinforced by analyzing the other prediction metrics, using the number of neighbors that leads to the highest R2 (that is, 6 for all the series and 5 for Boeing), we show the other prediction metrics in Table 6, to provide for a more complete picture of the prediction performance of the adaptive AI, and to be better able to evaluate the degree to which the topological structure of the underlying attractor contains exploitable information to predict the target risk variable.
| Correlation | RMSE/Amp | R2 | |
|---|---|---|---|
| SPY | 0.7816 | 5.72% | 60.34% |
| NASDAQ | 0.86 | 4.12% | 73.63% |
| Russell 2000 | 0.8295 | 5.11% | 68.53% |
| Lockheed Martin | 0.8563 | 3.31% | 73.06% |
| Boeing | 0.8611 | 3.12% | 73.96% |
| Airbus | 0.7716 | 4.20% | 58.82% |
Table 6: Prediction performance of the adaptive AI in one step ahead prediction.
As shown, in Table 6, in each case, we get a strong positive linear correlation between the AI’s predictions and the target series using the reconstructed attractor. For the NASDAQ, Russell 2000, Lockheed Martin and Boeing the correlation is higher than 0.8, for the SPY and Airbus the correlation is lower but near 0.8. This means that the AI’s predictions match well the daily trading sessions’ amplitudes’ fluctuations, so that it can be effectively employed in predicting these amplitudes, that is, there is exploitable topological information in the reconstructed attractor that allows the adaptive topological learner to predict the target series using the adaptive topological learner.
Considering, now, the RMSE divided by the data amplitude, we find, in all cases, that the RMSE is low when compared to the series amplitude, ranging from 3.12% to 5.72%. These results, along with the high R2 values show that there is a strong deterministic component in the system’s dynamics which is noise resilient, in this sense, we find that the reconstructed attractor’s topological structure can be effectively exploited by an adaptive artificial agent equipped with an adaptive k-nearest neighbors’ learning algorithm, further reinforcing the previous results on the presence of noiseresilient chaotic attractors underlying the daily trading amplitudes’ dynamics.
Regarding the predictability of each financial series we find that the results depend on the indicator, indeed, while all financial series have high predictability indicators, if we order them in terms of predictability, we find that, using the relative error indicator which is the RMSE divided by the series’ amplitude, the series with the highest error per series’ amplitude is the SPY (5.72%), followed by the Russell 2000 (5.11%), Airbus (4.20%), NASDAQ (4.12%), Lockheed Martin (3.31%) and Boeing (3.12%).
On the other hand, if we use the R2 score, we find that the worst performance is obtained for Airbus (58.82%), followed by the SPY (60.34%), the Russell 2000 (68.53%), Lockheed Martin (73.06%), NASDAQ (73.63%) and, finally, Boeing (73.96%). Despite the differences in the orderings obtained for two indicators, we find that there is a pattern that leads to two blocks in terms of predictability, in one block we have the SPY, Russell 2000 and Airbus, for this block, while showing a high performance in predicting the target series, the AI has a lower performance than for the second block which is comprised of NASDAQ, Lockheed Martin, and Boeing.
We expected the two financial indexes (Russell 2000 and NASDAQ) along with the ETF (SPY) to be less predictable than the single companies’ shares, since the financial indexes and the ETF can be linked to financial portfolios, with the SPY being linked to the behavior of the S&P 500, while the single companies’ data would tend to have stronger patterns. However, this hypothesis does not seem to hold, indeed, while the SPY and the Russell 2000 can be grouped together, the Airbus is also grouped in the less predictable group, while the NASDAQ is grouped in the most predictable group, furthermore, the NASDAQ is the second most predictable series in terms of the R2, which is a strong evidence against the hypothesis that financial diversification would lead to a lower exploitable pattern in volatility risk.
The presence of high-jumps in volatility and turbulence in the financial indexes implies that there are global synchronized dynamics, which is another relevant point regarding financial diversification and the diversifiable risk, namely, there is no fixed overall diversification risk reduction, instead, the diversification risk reduction depends upon the market phase, in the turbulent phase, the diversification risk reduction is lower.
So far, our empirical findings show that there is a strong link between the underlying reconstructed attractor and the target series, also, since the target series exhibits evidence of SOC, we find strong evidence of a form of stochastic chaos inducing SOC in the financial volatility series, a point that was argued and researched in [10] in an artificial financial market model.
From a risk science standpoint, our findings so far constitute a major example of the phenomenon of turbulence with fractal signatures typical of SOC having origin in an underlying noisy chaotic process, with a noise resilient low dimensional attractor, this hypothesis will be further reinforced by the topological data analysis that we will perform.
Addressing, now, the dominant dimension analysis, calculating the dominant dimension used by the topological learner, and using the permutation importance to calculate the importance of each dimension in the adaptive AI’s predictions, we begin with the SPY, the NASDAQ and the Russell 2000.
In Table 7, following the approach explained in the previous section, we show the chi-square test’s p-values for the equilibrium probabilities extracted from the Markov transition matrices for each subsample when compared with the full sample. As can be seen from Table 7’s results, the null hypothesis is not rejected for either subsample in the case of the SPY and Russell 2000 and, in the case of the NASDAQ, the chi-square test is only statistically significant for a significance level of 10%, with the null hypothesis not being rejected for a 5%, 2.5% and 1% significance levels. Overall, the results indicate that there is a dynamical stability of the stationary probability, in this way, we can proceed with the analysis of each equilibrium distribution.
| First half subsample p-value |
Second half subsample p-value |
|
|---|---|---|
| SPY | 0.483 | 0.4968 |
| NASDAQ | 0.0941 | 0.0873 |
| Russell 2000 | 0.4629 | 0.4628 |
Table 7: Significance levels (p-values) of the chi-square test for dynamical stability, obtained from splitting the full sample in two halves, for the SPY, NASDAQ and Russell 2000.
In Table 8, we present the Markov equilibrium distributions, rounded to the fourth decimal place, for the three financial series in order of increasing embedding dimension, these probabilities are the equilibrium distributions extracted from the full sample transition matrices shown in Tables 9-11.
| Dimension | SPY | Russell 2000 | NASDAQ |
|---|---|---|---|
| d0 | 0.212 | 0.1767 | 0.1202 |
| d1 | 0.1899 | 0.1705 | 0.1224 |
| d2 | 0.2034 | 0.1633 | 0.1272 |
| d3 | 0.2026 | 0.1687 | 0.1262 |
| d4 | 0.192 | 0.165 | 0.1266 |
| d5 | 0.1557 | 0.1238 | |
| d6 | 0.1335 | ||
| d7 | 0.1202 |
Table 8: Equilibrium distributions for the SPY, Russell 2000 and NASDAQ, extracted from the transition matrices shown in tables 9, 10 and 11.
| d0 | d1 | d2 | d3 | d4 | |
|---|---|---|---|---|---|
| d0 | 0.4653 | 0.1443 | 0.128 | 0.1343 | 0.128 |
| d1 | 0.1672 | 0.4035 | 0.1373 | 0.1505 | 0.1415 |
| d2 | 0.1382 | 0.1402 | 0.4472 | 0.1447 | 0.1297 |
| d3 | 0.1444 | 0.1314 | 0.1549 | 0.4379 | 0.1314 |
| d4 | 0.1262 | 0.1434 | 0.1448 | 0.1428 | 0.4428 |
Table 9: Transition matrix for the SPY, obtained from the full sample.
| d0 | d1 | d2 | d3 | d4 | d5 | |
|---|---|---|---|---|---|---|
| d0 | 0.3983 | 0.1173 | 0.1192 | 0.1185 | 0.1268 | 0.1198 |
| d1 | 0.1354 | 0.4102 | 0.1202 | 0.1202 | 0.107 | 0.107 |
| d2 | 0.1455 | 0.1317 | 0.3759 | 0.1124 | 0.1221 | 0.1124 |
| d3 | 0.1148 | 0.1242 | 0.1275 | 0.4192 | 0.1061 | 0.1081 |
| d4 | 0.1249 | 0.1133 | 0.114 | 0.1215 | 0.4014 | 0.1249 |
| d5 | 0.1252 | 0.1201 | 0.1288 | 0.1165 | 0.1302 | 0.3792 |
Table 10: Transition matrix for the Russell 2000, obtained from the full sample.
| d0 | d1 | d2 | d3 | d4 | d5 | d6 | d7 | |
|---|---|---|---|---|---|---|---|---|
| d0 | 0.3621 | 0.101 | 0.1044 | 0.1018 | 0.094 | 0.094 | 0.0661 | 0.0766 |
| d1 | 0.1009 | 0.3598 | 0.094 | 0.0974 | 0.1 | 0.0761 | 0.0974 | 0.0744 |
| d2 | 0.0987 | 0.0913 | 0.3676 | 0.0954 | 0.088 | 0.0913 | 0.0929 | 0.0748 |
| d3 | 0.083 | 0.0896 | 0.0954 | 0.3784 | 0.0929 | 0.073 | 0.1062 | 0.0813 |
| d4 | 0.0884 | 0.0876 | 0.0843 | 0.0843 | 0.3678 | 0.0983 | 0.0959 | 0.0934 |
| d5 | 0.0861 | 0.0878 | 0.0827 | 0.081 | 0.1089 | 0.3722 | 0.1038 | 0.0776 |
| d6 | 0.0745 | 0.0854 | 0.0893 | 0.0933 | 0.0752 | 0.1003 | 0.3793 | 0.1027 |
| d7 | 0.0792 | 0.0827 | 0.0957 | 0.0748 | 0.0836 | 0.087 | 0.1062 | 0.3908 |
Table 11: Transition matrix for the NASDAQ, obtained from the full sample.
As can be seen from Table 8, in each case, the Markov equilibrium probabilities are distributed close to the equiprobable distribution, corresponding to the inverse of the embedding dimension, with a few dimensions having a value slightly above the equiprobable distribution values and others below, which explains why the Markov equilibrium probabilities’ Shannon entropy is only slightly lower than the maximum entropy distribution, indeed, for the SPY, the entropy is up to a four decimal places approximation 2.3207 bits, while the maximum entropy is ln(5)/ln(2) which is approximately 2.3219 bits, for the Russell 2000, the entropy is approximately 2.5839 bits, while the maximum entropy is ln(6)/ ln(2) which is around 2.5850 bits, finally, for the NASDAQ, the entropy is approximately 2.9992 bits, while the maximum entropy is ln(8)/ln(2) which is equal to 3 bits.
The major implication of the Markov equilibrium distribution analysis is that there is no single dominant dimension in prediction, there is, instead, evidence of a Markov process transition between the dominant dimension in prediction importance for the topological learner. This evidence is contrary to a fixed linear autoregressive generator process for each trading session’s volatility, since such a process, upon delay embedding would imply that phase space dimensions would have fixed importance on the prediction of the target’s dynamics.
Considering, now, the companies’ data, for the chi-square test (Table 12), we find that the null hypothesis is not rejected for either subsample, in the case of Lockheed Martin and Boeing, and in the case of Airbus the test is statistically significant for a significance level of 10% and 5%, but not for a 2.5% and 1% significance. Again, there is evidence, in the case of Lockheed Martin and Boeing, of a dynamical stability of the stationary probability, in the case of Airbus there is some change in the sample, sufficient to reject the null hypothesis for a 10% and a 5% significance level, however, this change is insufficient to reject the null hypothesis for a 2.5% and 1% significance.
|
First half subsample |
Second half subsample |
|
|---|---|---|
| Lockheed Martin | 0.2972 | 0.3092 |
| Airbus | 0.0265 | 0.0278 |
| Boeing | 0.3508 | 0.3546 |
Table 12: Significance levels (p-values) of the chi-square test for dynamical stability obtained from splitting the full sample in two halves, for Lockheed Martin, Airbus and Boeing.
The equilibrium distribution for Airbus for the full sample is up to a four decimal places approximation equal to 0.5257 for the first dimension and 0.4743 for the second dimension, while for the left subsample these values are, respectively and also up to a four decimal places approximation, 0.5047 and 0.4953, and for the right subsample these values are, respectively, 0.5466 and 0.4534.
In Tables 13 to 16 we show, the equilibrium distributions extracted from the full sample transition matrices between the phase space dimensions (Table 13), the full sample transition matrix for Lockheed Martin (Table 14), the full sample transition matrix for Airbus (Table 15) and the full sample transition matrix for Boeing (Table 16).
| Dimension | Lockheed Martin | Airbus | Boeing |
|---|---|---|---|
| d0 | 0.5208 | 0.5257 | 0.1203 |
| d1 | 0.4792 | 0.4743 | 0.1315 |
| d2 | 0.1267 | ||
| d3 | 0.1257 | ||
| d4 | 0.1223 | ||
| d5 | 0.131 | ||
| d6 | 0.1297 | ||
| d7 | 0.1128 |
Table 13: Equilibrium distributions for Lockheed Martin, Airbus and Boeing, extracted from the transition matrices shown in tables 14, 15 and 16.
| d0 | d1 | |
|---|---|---|
| d0 | 0.6772 | 0.3228 |
| d1 | 0.3509 | 0.6491 |
Table 14: Transition matrix for Lockheed Martin.
| d0 | d1 | |
|---|---|---|
| d0 | 0.6675 | 0.3325 |
| d1 | 0.3686 | 0.6314 |
Table 15: Transition matrix for Airbus.
| d0 | d1 | d2 | d3 | d4 | d5 | d6 | d7 | |
|---|---|---|---|---|---|---|---|---|
| d0 | 0.3637 | 0.0983 | 0.0983 | 0.0923 | 0.0901 | 0.0896 | 0.0945 | 0.0733 |
| d1 | 0.1028 | 0.3724 | 0.1028 | 0.0924 | 0.0899 | 0.076 | 0.0859 | 0.078 |
| d2 | 0.0851 | 0.1031 | 0.3691 | 0.0907 | 0.0851 | 0.101 | 0.0907 | 0.0753 |
| d3 | 0.0884 | 0.0868 | 0.079 | 0.3671 | 0.0915 | 0.1097 | 0.0889 | 0.0884 |
| d4 | 0.0774 | 0.0977 | 0.0897 | 0.0961 | 0.3529 | 0.0966 | 0.0993 | 0.0902 |
| d5 | 0.0908 | 0.0858 | 0.0943 | 0.0853 | 0.0888 | 0.3696 | 0.0923 | 0.0933 |
| d6 | 0.084 | 0.0866 | 0.0881 | 0.0871 | 0.0926 | 0.0876 | 0.383 | 0.0911 |
| d7 | 0.0787 | 0.1094 | 0.088 | 0.0938 | 0.0938 | 0.1065 | 0.0926 | 0.337 |
Table 16: Transition matrix for Boeing.
Considering the Markov equilibrium probabilities (Table 13) extracted from the transition matrices (Tables 14-16), we find that, for Lockheed Martin and Airbus, the distribution extracted from the transition matrices for the dominant dimension in terms of permutation importance shows a similar profile with the first dimension having a probability slightly higher than 52% of having the highest permutation importance in prediction of the target series and the second dimension having a probability slightly higher than 47% of having the highest permutation importance in the prediction of the target series, therefore, in both cases, we have a lower but close to the maximum entropy Markov equilibrium distribution of 1 bit, with an entropy, up to four decimal places, of 0.9988 bits, in the case of Lockheed Martin, and 0.9981 bits, in the case of Airbus. In the case of Boeing, the entropy for the Markov equilibrium distribution is, up to a four decimal place approximation, equal to 2.9984 bits which is also close to the maximum entropy of 3.
In this way, we are again led to similar findings to those obtained for the ETF and the two financial indexes, namely, there is evidence of a Markov process transition between the dominant dimension in prediction importance for the adaptive topological learner.
The transition matrices for the two-dimensional attractors show a higher probability of the next dimension with highest importance being the current dimension with highest importance in prediction, so there is some persistence in the process. In the remaining cases, while the modal class, in the conditional probability distributions calculated in the transition matrices, is always the current class, there is a higher probability of a switch to one of the other dimensions as the most important in prediction in the next trading session rather than remaining with the same dimension.
Considering the results in context, we find strong evidence that the daily trading amplitudes for both the portfolio reference series and the individual companies’ stocks are characterized by underlying chaotic attractors with strong topological signatures that can be exploited by an adaptive k-nearest neighbors’ topological learner, and such that there is a transition between dimensions in terms of prediction importance, with the sliding window adaptive learning process, which means that the topological information associated with specific phase space dimensions for the next period prediction changes with time, which is an evidence more favorable to a nonlinear complex dynamics than to a fixed linear autoregressive dynamics associated with the delay embedding.
Now, considering that the adaptive topological learner extracted information from the k-nearest neighbors, the k-nearest neighbors’ topological data analysis is fundamental for a better understanding of the dynamical patterns. In this case, the main topological analysis tool is, as addressed in the previous section, the k-Nearest Neighbors’ graph (KNN graph) and the graph entropy measures evaluated by the degree relative entropy and the Kolmogorov-Sinai (KS) entropy as well as the graph’s degree distribution.
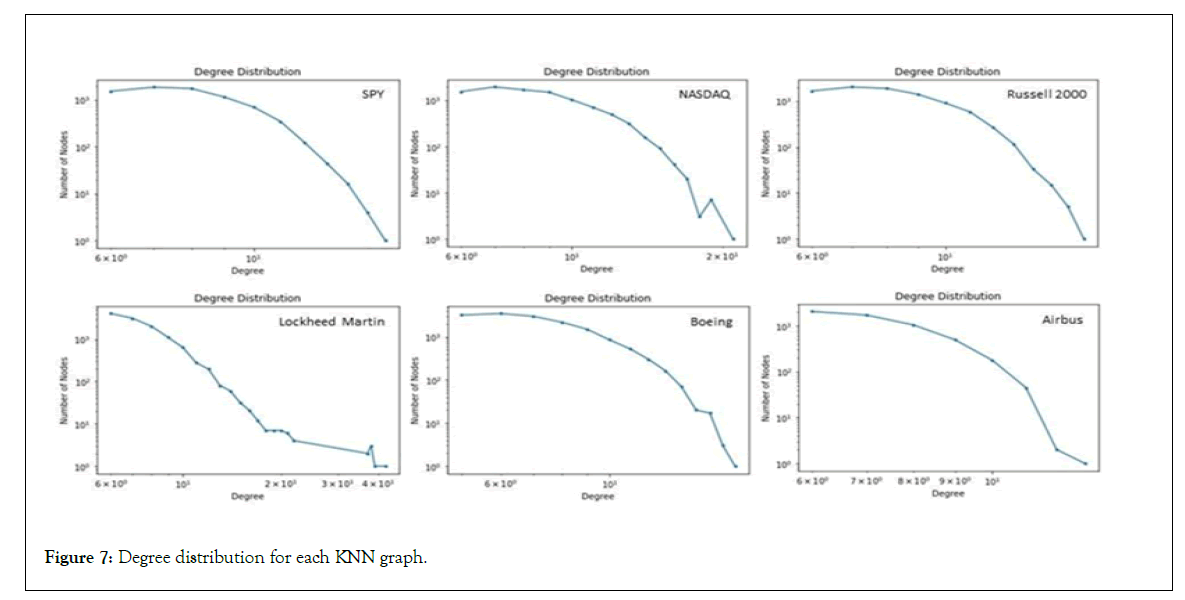
In this case, as can be seen from Figure 6, the reconstructed attractors’ KNN graphs show a complex neighborhood structure, considering the degree distribution, in Figure 7, we find an overall pattern that has a faster than power law decay, except for the case of Lockheed Martin, which shows a region of power law decay in the degree distribution. In this way, the topological structure of Lockheed Martin stands out over the other financial series’ KNN graphs, as a graph with a scale-free structure.
Figure 6: KNN graphs for each reconstructed attractor.
Figure 7: Degree distribution for each KNN graph.
In Table 17, we show the degree entropy relative to the maximum entropy [2,3], thus, scaling between 0 and 1, and the K-S entropy of these graphs. The degree entropy is far from 1, showing a far from maximum degree entropy value for any of the reconstructed attractors’ KNN graphs, the correlation between the two entropies, for these graphs is negative, but weak in strength, with a value of -0.2095, we also find, in the degree entropy, a strong pattern related to the predictability, and to the Lyapunov exponents, Hurst exponents and attractor dimensions, as can be seen from Table 18.
| Degree entropy | K-S entropy | |
|---|---|---|
| SPY | 0.1985 | 3.1545 |
| NASDAQ | 0.226 | 3.2756 |
| Russell 2000 | 0.2067 | 3.1921 |
| Lockheed Martin | 0.1801 | 4.1859 |
| Boeing | 0.2007 | 3.0331 |
| Airbus | 0.1641 | 3.0555 |
Table 17: Degree entropy and K-S entropy for each of the KNN graphs.
| Correlations | Degree entropy | K-S entropy |
|---|---|---|
| R2 | 0.5361 | 0.4045 |
| Hurst exponent | 0.5732 | 0.3318 |
| Largest Lyapunov exponent | -0.7301 | 0.7599 |
| Attractor dimension | 0.8849 | -0.4946 |
Table 18: Correlations between table 17’s entropy values and the R2, largest Lyapunov exponents, Hurst exponents and dimensionality of the reconstructed attractors.
From Table 18’s results, we find that the degree entropy is positively correlated with the prediction performance and the Hurst exponents as well, which means that the attractors with higher values of the degree entropy tend to be associated with the daily trading amplitude series with higher Hurst exponents and tend to be more predictable by the topological learner. These also tend to be the attractors with the higher dimensionality, indeed, the degree entropy is positively and strongly related to the attractor dimension, with a correlation of 0.8849, in a four-decimal places approximation. The K-S entropy shows weaker correlations with these three metrics, but it is strongly correlated with the largest Lyapunov exponent, with a correlation of 0.7599.
Indeed, considering the largest Lyapunov exponents, we find the difference in profile between the two entropy measures: The degree entropy is negatively and strongly correlated with the largest Lyapunov exponents (correlation of -0.7301) while the K-S entropy is positively and strongly correlated with the largest Lyapunov exponents (correlation of 0.7599). That is, the higher the value of the degree entropy, the lower tends to be the value of the largest Lyapunov exponents, while the higher the value of the K-S entropy for the KNN graph, the higher tends to be the value of the largest Lyapunov exponent.
This means that the two entropies provide for a different k-nearest neighbors’ topological profile analysis and connection to the main metrics. In this case, the higher the value of the degree entropy the lower tends to be the value of the largest Lyapunov exponent, the greater tends to be the exploitable topological information, persistence of the target series and the attractor dimension.
On the other hand, the K-S, which provides for the rate at which information is generated by the KNN graph, is, in this case, positively correlated with the exponential rate at which information is generated by the chaotic dynamics associated in this case with the exponential divergence of small deviations in initial conditions.
Finally, the degree entropy is also strongly and negatively correlated to the power law (fractal) scaling found in the histogram analysis, taken as the symmetric of the estimated slope in Table 2, the estimated correlation, not shown in Table 18, is -0.6315 which means that the higher the entropy value the lower tends to be the fractal dimension of the series’ distribution. This correlation is positive but low, in the case of the K-S entropy, with a value of only 0.2303. Therefore, again, the degree entropy values are the critical values in the relation to the main statistics.
Considering the full scope of the results, we find that there is a strong relation between the reconstructed attractors’ main features, including its topological features, and the target series’ dynamics, which reinforces the consistency of the findings in regards to CISOC underlying the dynamics of the daily financial amplitudes.
Conclusion
Smart Topological Data Analysis (STDA), combining chaos theory with topological data analysis and machine learning applied to the daily financial amplitudes of the SPY, NASDAQ, Russell 2000, Lockheed Martin, Boeing and Airbus allowed us to identify emergent low-dimensional noisy chaotic attractors with positive largest Lyapunov exponents and a strong topological structure that can be exploited by an adaptive AI system using a k-nearest neighbors’ learning unit and sliding window relearning, uncovering a strong predictability of the target series.
The evidence is of a form of stochastic chaos with low dimensional attractors underlying the long-memory and fractal scaling in the signal’s distribution, typical of chaos-induced self-organized criticality.
The STDA allowed us to link major topological features of the reconstructed attractors to the time series’ main properties, namely the fractal scaling in time and in the frequencies’ distribution. These findings reinforce two major lines of research within the complexity approach to finance and economics, the first being the fractal-based research pioneered by Mandelbrot the second being the chaos theory-based research.
Our results reinforce, in particular, Chen’s research into the presence of color chaos in the markets, and our previous research into financial market turbulence modeling using globally coupled chaotic maps that also induced SOC.
By calculating the dominant phase space dimension, from the permutation importance for the feature space comprised of the reconstructed attractor for the prediction of the daily amplitudes, used by the adaptive AI system, we found a pattern by which the adaptive learner’s dominant dimension changed with time.
These changes were found to be contrary to a linear autoregressive process that would be expressed by a simple autoregressive weighted sum over each degree of freedom resulting from the delay embedding, which means that the evidence is favorable to nonlinearities or possible interactions between degrees of freedom in the system’s dynamics. For the transition matrices between the different dominant dimensions in prediction, we found dynamical stability of the estimated stationary Markov distributions held in all cases at a 2.5% and 1% significance levels. These distributions were also found to be close to the maximum entropy, which, in this case, is close to a equiprobable distribution over the different phase space dimensions.
To better understand the attractor’s topological features we used KNN graph analysis and found a connection between the degree entropy of the KNN graphs and the prediction performance, largest Lyapunov exponents, Hurst exponents and the power law scaling in the daily amplitudes’ distribution. We also found links between the attractors’ largest (positive) Lyapunov exponents, the Hurst exponents, the attractors’ dimensions and the power law scaling of the distribution. These results allowed us to link the main attractor’s topological features to the SOC signatures, reinforcing the hypothesis of CISOC, also providing for an empirical example of CISOC, with direct links between the markers of SOC and the underlying chaotic attractors, which, in itself, is a relevant point for the study of SOC in complex systems’ science and in risk science.
From a risk science standpoint, the STDA methods employed in the present work to uncover and study a system’s dynamics associated with key risk variables can also be employed to other risk processes, in this way, the present work extends some of our previous works in epidemiology and, as stated above, links two major core theories for risk science: the theory of self-organized criticality and chaos theory.
It is important to stress that a stronger pattern in trading amplitudes, for the SPY, the NASDAQ and the Russell 2000 financial indexes, means that market turbulence in trading session volatility exhibits synchronized dynamics that is not diversifiable, which means that financial diversification, while relevant in reducing exposure to single asset risk, can still be insufficient to reduce risk exposure, especially, if the investment is focused on sector-specific stocks.
This last point is a mixed finding, since, on the one hand, it raises relevant issues regarding financial diversification, on the other hand, our results also mean that one can exploit the emergent chaotic dynamics and use the topological information to predict the next session’s volatility using the reconstructed attractor, in this way, risk management solutions for portfolio risk analysis need to consider the integration of STDA, chaos theory and the theory of self-organized criticality in their technological methods. Further studies are needed, however, to uncover more about the patterns of chaos in the daily trading sessions’ financial amplitudes.
References
- Gonçalves CP and Rouco J. Comparing Decision Tree-Based Ensemble Machine Learning Models for COVID-19 Death Probability Profiling. J Vaccines Vaccin. 2021;12(1): 1000441.
- Gonçalves CP. Low Dimensional Chaotic Attractors in SARS-CoV-2’s Regional Epidemiological Data. Int J Swarm Evol Comput. 2022;11(9): 1000271.
- Gonçalves CP (2023). Low Dimensional Chaotic Attractors in Daily Hospital Occupancy from COVID-19 in the USA and Canada. Int J Swarm Evol Comput. 2023;12(1):1000291.
- Mandelbrot BB, Fisher A, Calvet L. A Multifractal Model of Asset Returns. Cowles Foundation Discussion Papers. 1997:1164.
- Mandelbrot BB. The variation of certain speculative prices. In Fractals and Scaling in Finance, Springer. 1997:371-418.
- Mandelbrot BB, Hudson RL. The (Mis)behaviour of Markets: a Fractal View of Risk, Ruin and Reward. Basic Books. 2004.
- Voit J. The Statistical Mechanics of Financial Markets. Springer. 2001.
- Gonçalves CP. Financial Turbulence, Business Cycles and Intrinsic Time in an Artificial Economy. Algor Fin. 2011;1(2):141-156.
- Gonçalves CP. Quantum financial economics-risk and returns. J Syst Sci Complex. 2013;26:187-200.
- Gonçalves CP. Coupled Stochastic Chaos and Multifractal Turbulence in an Artificial Financial Market. Int J Swarm Evol Comput. 2022 11(7): 1000261.
- Schredelseker K, Hauser F. Complexity and artificial markets. Springer Science & Business Media. 2008.
- Palmer RG, Arthur WB, Holland JH, LeBaron B. An artificial stock market. Artif Life Robot. 1999;3:27-31.
- Lux T, Marchesi M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature. 1999; 397(6719):498-500.
- Farmer JD. Market force, ecology and evolution. Ind Corp Change. 2002;11(5):895-953.
- Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of 1/f noise. Phys Rev Lett. 1987;59(4):381-384.
[Crossref] [Google Scholar] [Pubmed]
- Bak P, Paczuski M. Complexity, contingency, and criticality. Proc Natl Acad Sci.1995;92(15):6680-6696.
[Crossref] [Google Scholar] [Pubmed]
- Chen P. A random walk or color chaos on the stock market? Time frequency analysis of S&P indexes. Stud Nonlinear Dyn Econom. 1996;1(2):87-103.
- Abbaszadeh MR, Nooghabi MJ, Rounaghi MM. Using Lyapunov’s method for analysing of chaotic behaviour on financial time series data: a case study on Tehran stock exchange. Natl Account Rev. 2020;2(3):297-308.
- Song X, Niu D, Zhang Y. The chaotic attractor analysis of djia based on manifold embedding and laplacian eigenmaps. Math Probl Eng. 2016;8087178.
- Gonçalves CP. Contributions to the categorical foundations of risk mathematics. 2010.
- Kaneko K, Tsuda I. Complex systems: chaos and beyond: chaos and beyond: a constructive approach with applications in life sciences. Springer Science & Business Media. 2001.
- Frey M, Simiu E. Deterministic and Stochastic Chaos. Comp Stoch Mech.1993:195-216.
- Puu T. Iterated Maps. Nonlinear Economic Dynamics, Springer. 1997:77-112.
- Schroeder M. Fractals, chaos, power laws: Minutes from an infinite paradise. Courier Corporation. 2009.
- Takens F. Detecting strange attractors in turbulence. In Dynamical systems and turbulence, Springer. 1980:366-381.
- Kaplan D, Glass L. Understanding nonlinear dynamics. Springer Science & Business Media. 1997.
- Handel PH, Chung AL. Noise in Physical Systems and 1/f Fluctuations. IOS Press. 1992:151-157.
- Fraser AM, Swinney HL. Independent coordinates for strange attractors from mutual information. Phys Rev A. 1986;33(2):1134.
[Crossref] [Google Scholar] [Pubmed]
- Eckmann JP, Kamphorst SO, Ruelle D, Ciliberto S. Liapunov exponents from time series. Phys Rev A Gen Phys. 1986;34(6):4971- 4976.
[Crossref] [Google Scholar] [Pubmed]
- Breiman L. Random forests. Mach Learn. 2001;45:5-32.
Citation: Gonçalves CP (2023) Chaos-Induced Self-Organized Criticality in Stock Market Volatility-An Application of Smart Topological Data Analysis. Int J Swarm Evol Comput. 12:331
Copyright: © 2023 Gonçalves CP. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.