International Journal of Swarm Intelligence and Evolutionary Computation

Spatio-Temporal Patterns Act as Computational Mechanisms Governing Emergent Behavior in Robotic Swarms

Terry Jack MDA, Khuman SA and Owa K De Montfort University, Leicester, UK
^*Correspondence: Mohammed D.A. Terry Jack, Glenburnie Road, De Montfort University, UK, Tel: +44-7852287613, Email:

Received: 01-Jan-2019 Published: 25-Feb-2019

Introduction

Main aims and challenges

The overall goal of this project is to intrinsically control the emergent behavior of a robotic swarm.

1st challenge: Conventional methods fail to control decentralized systems like swarms: At first, controlling a swarms behavior sounds straightforward enough, however, upon closer inspection it becomes apparent that this is a complex and nonlinear problem. Robotics warms are entirely distributed systems [1-5] with a distributed group intelligence [6]. This means that, rather than being focused within any one robot, the intelligence and control of a robotic swarm is equally distributed across all individuals [7] (a large reason why it is so hard to control a swarm). Furthermore, robots only have access to localized information gained through directly interacting with their neighbors (i.e., via contact or shortrange communication) and occasionally via indirect interactions (i.e., stigmergic signals left in the environment like pheromone trails left by ants).

Therefore, a swarm’s individual may even interact in a haphazard, disorderly manner, giving rise to the turbulent or chaotic characteristics of a swarm. Viewed at an individualistic level, robots can be seen busying themselves with their own, individual jobs; without a future vision and unaware of any larger picture [6]; they remain oblivious to the positive contribution their work and interactions are having on the global behavior of the swarm. Decentralized systems (like swarms [2,8]) coordinate in a manner completely alien to the norms of centralized control [2,6,9,10-12]. This means that robotic swarms are void of common control structures (like hierarchies, chains of command [1,2] or leaders-contrary to the misconception that the behavior of a swarm is somehow governed by the telepathic powers of a queen [13] etc). Unfortunately, centralized control strategies are highly dependent upon these infrastructures [12] and will fail when applied to decentralized systems which lack them. Ordinary control methods hold little influence over the governance of a robotic swarms behavior [1-6,8,14].

2nd Challenge [Extrinsic vs Intrinsic control]: There have been attempts at controlling robotic swarms by enhancing its individuals [6]. Under normal circumstances, swarms individuals are unintelligent and operate under very rudimentary conditions (i.e., have minimal processing power and are ignorant of global conditions pertaining to the swarm-such as their absolute position within the swarm [11]). If the robots were modified to have a more sophisticated processing power and enough memory to store an internal map or model of the environment, they could be programmed with the intelligence to estimate their own pose and location within the swarm (i.e., via Simultaneous Localization And Mapping-SLAM-techniques), and the swarm could essentially be controlled at the level of its individuals. This approach has been tested and produced accurate robotic behaviors (despite suffering minor difficulties when faced with very symmetrical environments such as corridors [11]), however, it is computationally expensive and ultimately requires the robots to be enhanced with more powerful, on-board processing [11].

To avoid increasing the robots computational power, which in-turn increases their complexity, expense and energy consumption (removing some key advantages of a robotic swarm), individuals have been modified to use off-board processing [11] (maps or models of the environment are stored externally and are accessed wirelessly by the robots during run-time). Therefore, robots need only be equipped with enhanced, long-range communication (something regular robotic swarms lack), which enables robots to access centralized, global information (i.e., GPS data [11], knowledge of the swarms overall goals or plans [15], the current state or behavior of the entire swarm etc. [3,11,12]) and thus forces a form of centralized control structure onto the robotic swarm. Unfortunately, this modification reduces the swarm’s adaptability (removing yet another advantage of a robotic swarm) since the limitations imposed by wireless transmission times and feedback delays [11] severely slow down the robots reaction times, making the swarm less adaptive in dynamic terrains with rapidly changing features [16].

Although a modified robotic swarm can perform feats such as splitting itself up into heterogeneous teams of robots which can then simultaneously solve sub-tasks which contribute to a larger, externally set goal, the resulting swarm behavior is very rigid (a piece-wise, stepby- step behavior), compared to the turbulent, organic, subtly selforganizing behaviour which emerges in unmodified robotic swarms (consisting of purely homogeneous, unintelligent individuals [6]). By attempting to tame a wild swarm (i.e., by imposing restraints upon it to control its behavior), it seems to cease behaving like a swarm. This suggests that enhancing a swarm’s individual in order to impose a centralized control structure on the swarm is not the secret to controlling its emergent behavior [3]. Controlling a swarm demands an alternative approach; one which avoids imposing any external influences and artificial structures onto the swarm [6,17]; the control must come naturally, from within!

3rd challenge (Emergent phenomena): Currently, designing emergent behaviors in robotic swarms is like working in the dark and relatively limited progress has been made. Swarm robotic designers have resorted to two main approaches which try to bypass the micromacro gap problem (i.e., how localized, individual behavior on the microscopic level lead to globally coordinated, intelligent behavior emerging at the macroscopic level) a bottom up behaviour based approach (which is timely and unsystematic) and a top-down evolutionary based approach (which is a black-box). If we are to ever, truly control a robotic swarm emergent behavior, an investigation into its Emergent Phenomena is inevitable. Researchers investigating Emergent Phenomena in Cellular Automata have discovered a hidden, computational layer which seems to bridge the mysterious micro macro gap. There is a lot left to explore in order to understand how computation emerges in many natural systems [18], however, we hypothesize that emergent computation is the secret to understanding the emergent behavior in robotic swarms (and likely all types of complex adaptive systems). Therefore, controlling the behavior of a robotic swarm (while retaining the high levels of independence demanded by the individuals within the swarm [3]) requires more insight into a robotic swarms rich, spatio-temporal information [19]. Swarms can be viewed as a form of parallel processing system, complete with inputs, outputs and an asynchronous spatial logic [2,20] which stores, propagates and modifies information across the swarm over time. The secret to unveiling (and eventually manipulating) the swarms mysterious self-managing behaviour lies in better understanding this intrinsic logic and inherent parallelism [10,12]. What are the mysterious mechanisms which link the micro-level components (which execute rules based on purely local information) to the subsequent structures and interactions that appear at the macrolevel? [17] If the information processing mechanisms which drive emergence and self-organization in robotic swarms can be uncovered, the understanding and insight gained would allow us to control artificial swarms [21] and perhaps even engineering new forms of parallel computing systems [10].

Sub-aims: There are several proposed tasks; each progressively more challenging than the last. Tasks are also accumulative; building upon prior tasks (hence the accomplishment of most tasks rest upon the completion of tasks preceding it

• Design a rule-set that produces intelligent, emergent behavior in a (stimulated) robotic swarm.

• Design a genetic algorithm that evolves a robotic swarm with emergent behavior.

• Discover the (hypothesized) computational mechanisms which underlie a swarm’s emergent behavior.

• Understand the computational mechanics discovered by: a. identifying all spatio-temporal patterns b. modelling the characteristic behaviors of each spatio-temporal pattern c. mapping the interactions between each spatio-temporal pattern.

• Predict the swarm’s emergent behavior by simulating its underlying computational mechanics.

• Investigate methods to manipulate the underlying computational mechanisms, including; (i) Injecting, (ii) Removing, (iii) Reflecting, (iv) Attracting and (v) Repelling spatio-temporal patterns.

• Intrinsically control the swarm’s emergent behavior by reprogramming its underlying computational mechanics.

Advantages to controlling a swarm

Not only is it beautiful to witness large numbers of individualspreoccupied with their own, self-serving objectives [3] effortlessly cohere and self-organize [1,6,8,14] into various emergent-behaviors [6,8], without realizing that their actions and interactions are inadvertently contributing toward a greater, global behavior [3,12], but robotic swarms also carry a number of advantages [10]. Complex problems are solved relatively easily with swarm-like strategies based on self-organization and emergent behavior [3], while conventional methods struggle [2]. Distributed control is also cost-effective [22] because any burden (i.e., power consumption, sensing and processing requirements [11], physical strength, etc) is shared equally across every individual. This is an especially attractive concept for aerospace systems since they must be limited in size, weight, and power consumption [3]. Yet despite individuals being small, limited and exhibiting very simplistic behaviors (like insects), a large number of them can culminate their abilities to form highly complex, intelligent group behaviors that are able to accomplish a wide range of significant tasks (e.g., robotic swarms inspired by ants can cross ditches by connecting to form a bridge [12]).

Most artificial systems are too rigid to operate under high levels of uncertainty and incomplete knowledge [6], commonplace conditions in natural environments. However, a robotic swarms ability to spontaneously reorganize itself makes it extremely flexible [1,12,14,23] and adaptable [3,6,22-24] to cope with a broad spectrum of situations, problems and tasks [12,25]. Robotic swarms can even respond to unforeseen events [1,6], even if the environment itself is dynamic (i.e., has continually changing features or conditions [6,23]). Even though the individual behavior of the robots are too basic to adapt or change, the resultant global behaviors which emerge across the swarm can flexibly adapt (e.g., a robotic swarm may spontaneously split into new group formations [6]). Adaptive systems also possess the potential to learn [6,14] (i.e., robot swarms may learn to favor a particular response when faced with a specific set of environmental changes [2]).

A swarms computational power is dynamic and can be increased (to solve more difficult problems) via the rapid deployment [22] of additional individuals injected into the swarm [20] (similar to increasing the number of neurons in a neural network to find better solutions to more complex problems). Likewise, for efficiency, only a fraction of the swarm need be used to solve simpler problems [20]. Since swarms are scalable to different group sizes [8,12,16,22,23], its global behavior is almost completely unaffected by the number of individuals within the swarm [22]. Hence, even if the swarm size changes mid-task (via the introduction or removal of individuals) its overall behavior does not drastically change [12] (other than a slight improvement toward larger set sizes [22]).

Networks of distributed individuals [22] like robotic swarms have the advantage of being robust [6,8,12,24,25] to individual losses [12], failures [16,23] and physical damage [1,14,20] and thus, even if individuals are added, removed or destroyed, the swarm is minimally affected [22]. Because communication in decentralized systems can occur between any neighbour [6] (rather than needing to communicate with a central entity and await new commands from them), the remaining individuals quickly re-adjust to compensate for any loss avoiding any significant effect on the final result [15] (which is why it is so difficult to exterminate social pests [12]). Robustness makes swarms very well suited to military applications. If space missions were conducted using swarms of miniature spacecraft [1] (as opposed to single spacecrafts), some members of the swarm could potentially sacrifice themselves for the greater good [1]. This natural fault tolerance [20,22] is largely promoted by redundancy [12], the absence of a leader [12] (in most systems, if the central coordinator is injured or lost, the entire system collapses [10]) and the strange fact that swarms (and other distributed systems) are only weakly sensitive to any one, individual influence [26] (a reminder that controlling an individual is not the key to controlling the swarm).

Finally, swarms can handle multiple inputs [4,5] and easily digest large amounts of information [1] by parallel processing it in an asynchronous manner across its large collection of individuals. By dispersing the information across the entire system [1], as opposed to bottlenecking the data (as is done during linear (centralized) information processing [10,24]), higher information exchange rates [27] can be achieved at great speeds and efficiency.

Applications of controlled swarms

It is a wonder how swarms ever synchronize their decentralized information to come to a common decision [12] or make group decisions and think as a whole. Yet they can and do. Examples of such collective decision making behaviors include: task allocation, consensus, collective counting [28], collective memory [28], etc. Swarms can perform incredible feats, otherwise over burdensome for a single individual, due to their pooled resources. Collective transportation (wherein individuals cooperate by connecting to increase their overall pulling power) is useful for carrying large, heavy objects [9,12], such as gallons of water or chemicals to pollinate a field of crops [1]. A simple lattice formation [22] can be very useful to quickly establish a distributed computer grid (also known as a distributed sensing grid [22]). Applications include:

A dynamic, emergency communication network [3] ideal for situations where traditional, stable network Infrastructures (i.e., satellite communication) have broken down [1,2] or become inaccessible due to extremely long distances or barriers [3]. An emergency communication channel is a primary security requirement in disaster relief scenarios. Multiple tiny robots quickly disperse into the open spaces. Upon detection of a survivor, a robot emits a message signalling the discovery. This message is propagated locally between robots only... (and) makes its way back to the entrance where rescue team members can now follow (it)... to the survivor [16]).

Surveillance [1,12,16,22] an obvious application due to its wide use in reconnaissance [16], traffic monitoring [1], image processing [28,29] and weather and climate mapping [1].

There are various other safety, security and environmental applications [1,2] including: intrusion tracking [12,16], hazardous environment exploration [1] (e.g., NASA is investigating swarm based spacecraft to explore deep space without risking human lives [3]) or hazard detection [16] and removal (e.g., removing old landmines [12]. swarms of tiny (robots)... explore the ocean floor and clean up the marine bays [3]. Equally by detecting and cleaning up harmful chemicals, pollutants and oil spillages [1,2,12]) as well as its future maintenance. iv. A distributed display (each robot serving as a pixel in the display) embedded in the environment and actively annotating it (e.g., terrain features may be highlighted or added, such as synchronized blinking lights to form a route toward a site or person, etc) [16]. Swarms are probably most known for their mystically selforganizing computational geometries [28]. Randomly distributed individuals will automatically and spontaneously organize themselves and their surrounding objects [12] into orderly formations. Spatiallyorganizing behaviors [22] that manipulate the environment can be useful for assembling physical constructions [12,25,30] such as those built by bees, termites and other social insects [17] or alternatively for the assembly of complex, large-scale, virtual systems [6]. Spatiallyorganizing behaviors that focus on manipulating the swarm itself can be used for morphogenesis [12] (self-assembly [20]) which includes self-management, self-optimization, self-protection, self-healing or self-repair [3,20,22], self-configuration [3] and self-construction [6]. The most common spatially-organizing behaviors include (a) aggregation [9,17,25] (often seen when social animals flock [12] or swarm [25] together), (b) dispersion or splitting up (a form of predator avoidance [14,25] often utilized in schools of fish or motorcycle gangs being chased by the police), (c) segregation [17,30] which can be used to sort, group and cluster together different classes of objects [17] into patches, bands (as with annular sorting) or any other geometrically organized formations. For this reason, this is sometimes referred to as shape or pattern formation which can be extended to chain formations and bulk alignments [25], all of which have numerous applications for civil defence (i.e., automatic perimeter defences [22]) and offensive military operations (i.e., battlefront formations [30], convergent attacks on targets from multiple sides [3], etc).

A swarms ability to self-organize can produce many beautifully unified swarm behaviors such as coordinated motion [9] (to increase stability when travelling through rough terrain [12]), and foraging [9,14], collective exploration [1], path planning and other navigation behaviors [3,12,28,29] which have inspired efficient search methods and optimization algorithms (e.g., ant colony optimization, bird swarm algorithm, etc.) due to their rapid terrain coverage across expansive environments (or virtual search spaces) via their inherent pluralization and redundancy [11]. Thus, swarms would serve well in search and rescue operations required in the aftermath of a natural disaster [1,12].

Eventually, as the field of nanotechnology advances, swarms of nanobots could be used in health care [1,2] (like an artificial immune system-just as virtual swarms are already being utilized to defend and optimize computer networks, by automatically rerouting and repairing nodes, discovering and attacking malicious viruses, etc. [6]). As well as targeting natural ailments and foreign viruses, they could improve or enhance our own bodily functions. They could even potentially discover and kill cancer tumors [3].

Dangers of uncontrolled swarms

Despite the ability swarms have to scale, if the number of individuals in the swarm becomes too little, the intelligent group behavior of the swarm disappears and only the simple, unintelligent behaviors of the individuals remain (this is why it is impossible to understand a swarm’s emergent behavior by studying the individuals in isolation). Large numbers are required for intelligent swarm behaviors, such as self-organization, to emerge [30].

There are two large disadvantages which discourage a wider acceptance of swarm usage, both due to the unpredictable nature of a swarm. Firstly, the time taken to converge to the desired, global behavior varies greatly for each run; it can sometimes converge very quickly and sometimes very slowly. This is because the convergence speed is dependent on the combined feedback times between neighboring individuals communicating within the swarm and any subsequent spatiotemporal pattern propagation transporting, converting and combining local behaviors across the swarm [7] (which can be significantly slow depending on the spatial medium for instance it took several days for slime mold in a petri dish to produce a voronoi diagram [20]). Secondly, the flexible, adaptive nature of swarms mean that their global, collective behaviors are difficult to predict. They often vary with different environmental conditions, despite individual level behaviors within the swarm remaining the same [13]. This unpredictable adaptability poses sophisticated management challenges to controlling a swarm [2] and it is widely accepted that controlling a swarm (i.e., changing its global goal [6], stopping it if it is behaving too dangerously [12], etc) once it has started operating is not yet possible [12]. Thus far, most control features of true swarms have been to design global behaviors and features into the swarm during its design phase, prior to its deployment and execution within the environment [6]. Nevertheless, it remains the ultimate goal of this project.

Until a method to properly control swarms during runtime has been developed, it is far too risky to deploy them among humans [12] due to the potential threats they pose over safety, security and confidentiality [2]. Furthermore, a swarm can be viewed as a mobile dynamic network, and thus faces the many risks associated with networks (e.g., Cyber-attacks to the physical, software or network layer of the swarm could easily disrupt communication links between mobile-robot nodes). The emergent behavior of the swarm could potentially dissipate if its network were significantly disrupted.

Background

Robotic swarms

A single robot is an autonomous system in itself [3,6,12] requiring minimal manual intervention during runtime [12]. Robots are thus well suited for remote exploration missions in hazardous locations with harsh conditions (i.e., deep space [3]) or other jobs that are considerably risky and dangerous for human beings. A robotic swarm is a multi-robot system [1] and is thus comprised of multiple autonomous individuals [2] (often large numbers [2,3,12]; in the thousands [3]). Whereby a single robot can only carry out a linear sequence of tasks, a robotic swarm can break up the list of tasks and distribute it across the swarm to be completed in parallel [17], completing the job more quickly, easily and efficiently.

Robotic swarms vs. Collective robots

However, swarm robotics is not the same as other approaches to collective robotics [12]. The robots in a robotic swarm are extremely basic, simple and reflexive individuals [3,12] that merely react to sensory stimuli [12] (they do not direct their work but are guided by it [17]). They are extremely unintelligent robots [16]; they have no memory of past actions or previous state information [16,31] nor any internal models to map their current environment or represent their present states [11,16]; and since they have no memory or models to plan and predict future actions [12], they are incapable of sophisticated [14], goal based behaviors; unable to proactively plan ahead, make complex decisions or solve problems individually [2]. Furthermore, individuals in a robotic swarms do not have long-range communication [11] (nor global information like global positioning, by extension) and are limited to communicating locally (i.e., with nearby neighbors rather than the whole swarm) via direct interactions [3,6,11,12,15,16,32] or via short-range sensors primarily used to detect immediate surroundings (e.g., infrared [32], virtual pheromones [16], etc.).

Robotic swarms vs. Emergent phenomena

The major advantage of such simple individuals [6] is that each robot requires minimal on-board processing [16] and only a basic processing power which is advantageous for miniaturization [3] (robots can potentially be the size of dust particles [16] if coupled with advances in nanotechnology). What’s more, a society of low-level individuals cooperating re-actively behaves intelligently as a collective, and complex tasks are solved in ways superior to solutions planned in advance via conventional, proactive, high-level methods [1,14]. This artificial swarm intelligence [3,14] emerges without any active push for it at the individual level [3] nor via properties from any single individual [14] and gives a whole new meaning to the age-old cliche the whole is more than the sum of its parts [6]. The emergent behavior [1,2,8,12,33] of swarm robotics destroys the assumption that individuals obeying simple rules can only ever produce simple behaviors [34]. Complex global behaviors need not result from complex rules [34] as they can also emerge from very simple rules [3,12,15,33] as demonstrated by the many natural systems from which swarm robotics draws inspiration (e.g., birds do not plan or knowingly cooperate to collectively fly in a v-shape, rather each bird focuses on simple rules like flying at a certain speed and proximity relative to adjacent birds [34]).

Emergent phenomena

The ability for natural systems to create order from chaos has gained the attention of a large body of academic researchers and spawned a whole new cross-disciplinary science, called complexity science or complex (adaptive) systems, devoted to understanding this phenomenon. Yet an emergent phenomenon is still not fully understood, despite being at the forefront of current research. It is not well understood how such apparent complex global coordination emerges from simple individual actions in natural systems or how such systems are produced by biological evolution [10] and thus understanding and harnessing the fundamental organizing principles of emergence remains one of the grand challenges of science [35].

What makes emergent behavior so difficult to understand is that, unlike resultant behavior, the systems global behavior is counterintuitive since it is not a property of any of the components of that system [34] and thus shows no correlation to the individual behavior of the individuals making up the system [34] (e.g., analyzing the behavior of an ant will reveal nothing about how ant swarms are suddenly able to self-organize into an ant bridge). When analyzing the local behavior of any one individual, the emergent phenomenon disappears. If an emergent phenomenon is to be studied, it must be done by analyzing the distributed individuals in parallel. This may be hard to comprehend because people have a centralized and deterministic mindset, they expect there to be a centralized leader (a bird leading the flock, a queen bee controlling the hive, etc.) and are uncomfortable believing that randomness can sometimes give rise to orderliness or patterns [36].

Examples of emergent phenomena in nature

Emergent behavior is a mysterious, natural phenomenon which allows a group of randomly distributed individuals lacking any global information, intelligence, or global communication (via a central controller) to spontaneously self-coordinate into an organized collective group, capable of a coherent, intelligent behavior (e.g., emergent phenomenon transforms a collection of simple neurons into a complex, intelligent brain that can produce abstract thoughts). It is believed that emergent phenomena, like group learning, artificial evolution [9], global organization and self-coordination, are all sideeffects of individuals communicating with one another, explicitly and implicitly, in a decentralized, swarm-like manner.

Self-organizing, group behaviors emerge across physical [26,30], biological [3,30] (insect [1,2,8,13,25,30] or animal [2,8,12,30]) and sociological settings. Physical systems may include stable magnetic orientations and domains [26] or vortex problems in fluids [26], etc. Biological systems include single celled organisms [25] which exhibit emergent behaviors when in large groups (such as the spontaneous aggregation of bacterial colonies [10,12], or the subtle adjustment of tumbling rates due to the perceived chemical concentrations which allows bacteria to move toward regions rich in nutrients [15]). Larger living organisms (like humans) are but a collection of cells, selfassembling and interacting locally [19] to form tissues, [12], organelles [7], organs [12], organ systems and other necessary body systems (such as the immune system-which has inspired many network intrusion detection algorithms [6]). The brain (which has inspired the creation of Artificial Neural Networks) is nothing more than a large collection of specialized cells called neurons [10] that interact locally (by exchanging electro-chemical signals [37]) to parallel process external sensory information [10] via emergent computations [38], resulting in our internal thoughts and emergent mental images [38].

Emergent phenomena is also rife in social systems like insect colonies, such as flies [39], fireflies (which are able to flash together, synchronously), spiders [6], cockroaches [12], termites [12,16,17] wasps [14], bees [6,12,14,15] and ants [3,6,12,14-17,40] (which are by far the most commonly studied social insects). In particular, the way ants forage (which has inspired network routing optimization), build nests, sort their brood (eggs are sorted and grouped by developmental stage [17]), manage their dead (experiments involving the random distribution of dead ants will result in workers forming clusters within a few hours [40]), divide their labor (inspiring task allocation solutions), self-assemble (physically connecting to build bridges, rafts, walls and bivouacs [12,18]), make collective decisions, come to a consensus (deciding between the shortest of two paths [12]) and implicitly cooperate (i.e., to carry heavy food). Similarly, emergent phenomenon readily occurs in animal societies, such as schooling fish [12,14,15,25,40,41], flocking penguins [12], migrating birds [3,12,25,40,41], herding gazelles [41] and many other social animals [25]. Crowds [15,25] and mob mentalities [7] are some examples of emergent phenomena which often occur in human societies [6,36].

According to Physicist David Bohm (in his theory of implicate and explicate order [42] which elegantly resolves long unanswered questions in the field of Physics such as how is quantum physics and general relativity unified? How does quantum entanglement allow for faster than light communication? etc.), reality itself is nothing more than an emergent phenomenon! The explicate order (each temporal moment in our spatial reality) is a surface phenomenon-an emergent projection that temporarily unfolds out of an underlying implicate order [43]. This idea concurs with earlier revolutionary ideas supported by Physicists Stephen Wolfram [44] and Richard Feynman, which state that the entire Universe is parallel processing information via emergent, spatiotemporal computational structures, like those found driving emergent phenomena in cellular automata.

Important conditions to establish emergence

Sociology is not just applied psychology, just as psychology is not applied biology, nor is biology applied chemistry, neither is chemistry applied physics, nor is physics merely applied quantum mechanics [34]; The whole is greater than the sum of its parts. The extra bit is the consequence of how the parts interact [34]. At the ground level, the action of one individual activates another individual, like a chaotic chain-reaction (which is why this process is sometimes referred to as chaining). In this manner, a system of individuals (who only require rudimentary reasoning [40] themselves; enough to react to external stimuli) is able to behave intelligently as a collective by executing sophisticated rule-chains constructed via the complex, parallel chaining of numerous such individuals. However, chains of interactions won’t necessarily produce emergent phenomena [34]. Or if it does, it may not necessarily be emergent behavior which is intelligent and useful. Some systems only exhibit globally emerging patterns which seem to be no more than aesthetically intriguing rather than more advanced emergent behaviors like the type whereby individuals can self-organize to solve complex task, perhaps only producing patterns as a side-effect (e.g., ants foraging, termites constructing nests, etc.).

If a systems behavior can re-influence the original system (i.e., there is feedback [6,13,21,34]), then the systems behavior begins to modify itself dynamically, becoming nonlinear in the process [34]. Positive feedback reinforces and amplifies certain behaviors [13] (promoting the creation of structures via a snowball effect [21]) whereas negative feedback is like a regulatory mechanism [21] which stabilizes patterns and counterbalances positive feedback [13]. Nonlinear [23,26,34] interactions [23,34] are a key element to establishing intelligent, emergent, self-organizing behaviors. This (coupled by an element of randomness [13]) is why emergent behavior is near impossible to predict [6] at the level of the individual. Thus, the secret to unveiling emergent phenomena does not lie within the swarms individuals, but within their (spatio-temporal) interactions [6,12,15,26,34].

Understanding emergent behavior using cellular automata

Similar lines of research into understanding, controlling and predicting emergent behavior have been conducted using a number of distributed systems other than robotic swarms. The most popular distributed systems used (due to its relatively simple nature) are Cellular Automata (a group of virtual cells with a discrete size conserved number and fixed position. They can only really change their states, and the simplest CAs only have binary states; dead or alive; black or white; etc). The majority of these studies is focused only in the one-dimensional (binary) CA [45] which is just a 1D row of virtual cells (as opposed to a 2D lattice) since it is important to study how this phenomenon emerges in even the most basic complex system [46]. Using a simplistic representation that maintains the most important features of the complex system being modeled [5] makes the task of understanding a complex concept like emergent computation easier and clearer [10,31,39]. The general principles behind how complexity arises from simple rules and many of the secrets behind emergent computation have been revealed through studying 1D CAs [5,6,47]. A lot of progress was made when studying 1D binary CAs evolved via a Genetic Algorithm (GA) [10,48,49] to perform intelligent emergent computations such as calculating its own global density (the classification task); i.e., the CA must decide which state are the majority of the cells at the start (the density of its initial configuration) and then slowly make the CAs final configuration (output) into that state globally (e.g., if the majority of cells in the initial configuration were alive, then the final configuration should transform all cells to become alive, and vice versa) [49].

Bare in mind that this is no trivial task for a 1D line of fixed cells which can only communicate its binary state to its nearest neighbors. Nevertheless, researchers have also extended their studies of emergent phenomena to 2D Cas [24] (an example of an emergent phenomena in 2D CAs is object boundary detection in images. A 2D CA can achieve this fairly easily using the majority rule - i.e., a cell adopts the same state as the majority of its neighbors [24]). CAs update their cells states based on predefined update rules (i.e., a look-up table which defines which state a cell should change to base on its current state and the states of its neighboring cells [37]). Some update rules have been noted to produce Emergent behavior, while others do not. Thus, different update rules have been classified into four distinct classes [44] based on the global CA behaviors they produce.

Class I: Fixed point attractors and class II: periodic-attractors both have short-lived transient times and converge too soon to produce dynamic behavior; quickly collapsing into orderly homogeneous (class I) or heterogeneous (class II) states. Class IV: strange-attractors (a.k.a. the edge of chaos [50]) has a long, indefinite transient time and eventually converge into complex states; although it is globally disordered, embedded sites of order emerge. Class III: chaoticattractors have infinite transient times and never converge because it diverges into random, aperiodic states of chaos. Only classes III IV can create the correct conditions for emergent behavior because emergence can only occur in the fluid transient time before the system solidifies into a converged state [50-54]).

Collision-based computing

Collision-based computations [28] (a.k.a. computational mechanics) offer a convincing theoretical explanation to explain intelligent, self-organizing, global behaviors (i.e., make decisions, remember, classify, categorize, generalize, recognize, problem-solve, correct-errors, etc. [26]) in cellular automata [10]). The theory views complex systems (including robotic swarms) as decentralized networks of emergent information processors [26]; architecture less computers (as opposed to conventional, von-Neumann type, central-processing computers). Individuals within the complex system indirectly (and unknowingly) communicate with one another via an embedded computational layer composed of dynamic, spatio-temporal structures that serve to parallel process information across the entire complex system [10,24]. This means that even in the absence of a central controller and access to global information, individuals within the distributed system can still communicate globally via this embedded, computational layer. The essence of collision-based computations are nonlinear logical operations [26] performed by emergent information processing elements; spatio-temporal patterns which parallel process information [10]. Without these emergent spatio-temporal patterns, information processing could not occur, since the alternatives would either be too ordered and unchanging to transport or modify information [18], or too dynamic and changing to store information long enough to modify or transport it. So what exactly are these fundamental spatiotemporal patterns and from whence do they emerge?

Embedded spatio-temporal structures

During investigations into the emergent behavior of 1D CAs, solid, long and narrow structures [47] (termed particles) were seen emerging from localized dynamic regions of chaos (chaotic regions seem to be favoured over static, orderly regions due to their random perturbations which act as nucleation sites [47] from which the embedded, particle structures grow via smaller proto-particle structures [47]). Similar discoveries were soon made in 2D CAs too (Conways Game of Life is a famous example of a 2D CA with a rich variety of spatiotemporal patterns more commonly known as gliders, the 2D CAs equivalent of a 1D CAs particle). These emergent patterns (also referred to by various names across the vast yet scattered body of research literature attractors/stable points [26], distributed embedded devices [6], vehicles [47], embedded structures [28], momentary wires [29], signals [19,29,39,47], communication blocks [19], virtual particles [22], gliders [28,37,47,55], gestalts [26], domain boundaries/walls [10], mobile selflocalizations [28], wave fronts/fragments [28,29,55], travelling temporal structures (regional boundaries) are not explicitly represented in the system [24] since they are embedded within the nonlinear interactions of individuals and are only revealed via analyzing the spatial interactions over time. We could even say that these spatio-temporal patterns are the underlying dynamics of emergent behaviors [10,15] and the fundamental processors [10] of emergent collision-based computations and the driving force behind global emergent phenomena (the interactions are merely the carriers or media in which they exist and the links themselves only existing as a result of the physical individuals interacting, making it a 3rd order entity, or 2nd order emergent phenomenon).

Representing and storing information: Spatio-temporal structures (e.g., virtual particles in 1D CAs, or gliders in 2D CAs) come in different, unique patterns, each representing specific pieces of information [10,19]. The data are stored in the system so long as these structures persist (like a memory [10,19,39]). Researchers studying the computational mechanisms of 1D CAs managed to identify five unique stable particles (spatio-temporal patterns), which they labelled as [10], and curiously, one unstable particle [10], which suggests some spatiotemporal structures spontaneously change (i.e., their patterns or velocities) without any external influences. However, the majority of spatio-temporal structures are stable and require an external event to drive a change.

Transferring information: Information is transferred across the system via the spatio-temporal pattern propagating over time [10,19,24]. These spatio-temporal structures are essentially emergent signals used to process, store and communicate information across the system, with its medium of travel being the system itself [19]. Therefore, almost any part of the mediums space can be used as a (momentary) wire-a trajectory of (a) travelling (spatio-temporal) pattern [28,29]. Each spatiotemporal structure will have a set velocity (speed and direction) at which it propagates through the system [10,19,24].

Modifying information: Information is modified if the spatio temporal pattern representing it becomes modified and so to changing a pattern is how to change data [10,19]. Spatio-temporal patterns (as well as their velocities) are most commonly changed via collisions between two or more spatio-temporal structures [5,18,51]. Collisions change the structures velocity and pattern according to an intrinsic logic specific to that system [5,18,51]). Interestingly, collisions always follow a deterministic logic (e.g., spatio-temporal patterns and always produce spatio-temporal pattern upon collision). This means that spatio-temporal structures travelling and interacting (i.e., colliding) in space form the basic logical operators of (dynamic, massively-parallel, architecture-less, collision-based) computation [10,28,29,47]. Logical collisions correspond to computations that transform the data. Logical operations occur at the place where the spatio-temporal structures collide, annihilate, fuse, split or change direction (these sites correspond to the logical gates) [29] and various forms of logical gates are realizable [28,29] (including xor gates and diodes [29]). The presence (or absence) of spatiotemporal structures represent the Boolean truth values of logic gates [28,29]. Collision-based logic-gates typically have inputs corresponding to the presence of the colliding spatio-temporal structures. Its outputs correspond to all the possible outcomes of their interaction, including and output resulting from non-collisions (i.e., the output will be the same as the input) [29]. To generate dynamics representing basic logical operators (is) the foundation of computation [47].

The research into emergent phenomena in CAs has inspired the theoretical foundations of our investigation into the underlying mechanics of emergence of robotic swarms. It is not unreasonable to hypothesize a parallel system of embedded spatio-temporal structures underlie the emergent behaviors of robotic swarms since there have been odd reports to suggest that such computational mechanisms exist for complex systems other than CAs. For example, structures that propagate in a coherent direction and speed [55] have been experimentally manifested in a chaotic 2D chemical media (BZ mediums [28]) and its behavior and computational dynamics are comparable to those of 2D cellular automaton. As wave-fronts in the chemical media expand, their collisions produce new wave-fragments in a deterministic manner [55]. Thus even physical media are capable of collision-based computing, since the collision of spatiotemporal structures emerging in their space-time evolution are represented by interacting wave fragments geometrically constrained to the chemical medium [28]. Unlike simulated 2D CAs, however, the emergent structures in the chemical media disintegrate after some time. Stable spatio-temporal entities (more popularly referred to as gestalts [26]) have also been observed emerging in the flow of (discrete or continuous) phase spaces in artificial neural networks. Gestalts store information in their locally stable structural configurations and act as a form of memory [26]. Various classes of flow patterns are possible [26] and likewise, if these local stable points can be induced (or manipulated) the neural network could be controlled and a specific memory could be assigned [26].

Test Methodologies

Computer simulations

The swarm’s emergent behavior eventually needs to be analyzed for spatio-temporal structures and early analysis favours computer simulations [6] because the simplicity offered by computer simulated models can be advantageous; realism is not necessarily needed or helpful [56]. Simplification allows us to focus on features which truly concern us and can lead to greater insights. Furthermore, the cost of scaling up the number of robots is not a main concern for multi-robot simulators [12] and since a swarm can behave very differently at different sizes, having the freedom to increase the number of robots in a swarm is quite important during initial experimentation. Lastly, the exact same experiment can be repeated very easily in simulations and temporal elements can be manipulated if needed (i.e., paused, sped up, etc) to allow for quick overviews of a swarms developmental patterns or more careful observation of pivotal points during experimentation [30,36] (Figures 1-5).

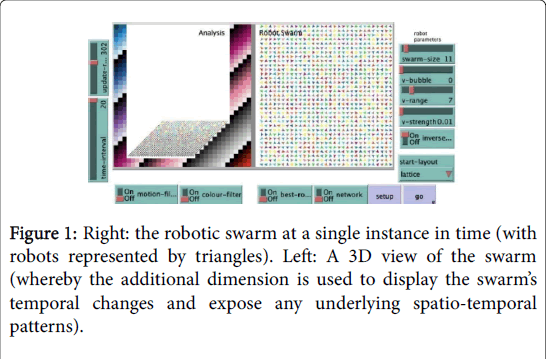
Figure 1: Right: the robotic swarm at a single instance in time (with robots represented by triangles). Left: A 3D view of the swarm (whereby the additional dimension is used to display the swarm’s temporal changes and expose any underlying spatio-temporal patterns).

Figure 2: The robotic swarm modelled as a dynamic network. The network nodes represent the position of the robot while the connections represent their local influences on neighboring robots.

Figure 3: Examples of the robotic swarms emergent behaviour using the voronoi rule-set. Left: At start, all robots (represented by triangular particles) are randomly scattered across an environment with obstacles (represented by circles). Right: At end, the swarm self-organizes itself to boundaries (resembling cell walls) segregates each obstacle (resembling nuclei).

Figure 4: Three snapshots in time of the robotic swarms formation when running on the virtual-forces behavioral rule. Regardless of the individual robots starting positions, the robots always selforganize into orderly lines as shown above.

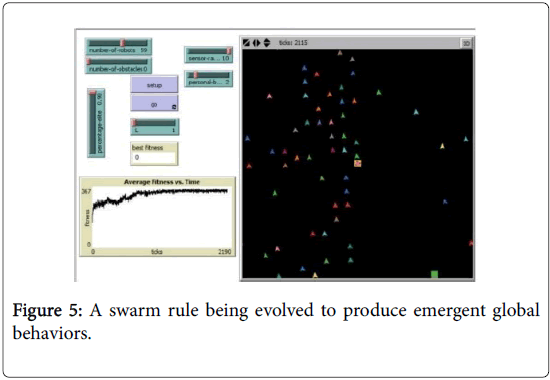
Figure 5: A swarm rule being evolved to produce emergent global behaviors.

NetLogo

The robotic swarms used in this project were all evolved, modelled, simulated and analyzed using the multi-agent programming language called NetLogo. NetLogo is the language of choice for modelling complex adaptive systems and emergent phenomena [36] because it was designed for the efficient computation and representation of thousands of heterogeneous individuals running in parallel [36].

Modelling the robotic swarm across space

Particle swarm representation: The most straight forward way of modelling a robot swarm in a computer simulation is to represent each robot as a single point (a particle) which can move around on a 2D landscape. By representing the robots as simple point particles, we minimize the computational burden [36] to allow resources to be directed to more important areas of the simulation (i.e., the execution speed, etc.) [30].

Dynamic network representation: The great number of interacting individuals in a robotic swarm can be viewed as a dynamic communication network [11,12], (each simple robot acts as a mobile node that become spatially and/or temporally interconnected via shortrange communications) and thus it is not uncommon to refer to robotic swarms as distributed, robotic sensor networks [2,11] or mobile, (parallel) computer networks wherein robots act as embedded sensing and processing elements in the environment [2,11,16]. Viewing the swarm as a dynamic network (wherein each node represents a robot and each link represents the local robot influences on one another) can aid understanding of how the swarm is interconnected. Explicit interaction refer to direct actions or interactions between individuals [3,12,14] (i.e., robot-robot interactions [8,14]) including direct communication via close-range sensors within a local neighborhood [16] (e.g., shining light [15], colored LED displays, infrared, audio and acoustic signalling, coil induction, radio-frequency broadcasted messages, body-language, sign-language, colored patterns on robots [2], robot recognition [32], and other indirect clues such as the perceived density of the robot population or net force of robots on an object [12], etc). Implicit interactions, also known as robotenvironment interactions [8,12,14] or stigmergic communications [2,8,40], refer to indirect links formed after a short time delay from the robots initial signal. Since the external environment can also act as a stimulus to affect the behavior of individuals [47], the environment can be manipulated by structurally modifying it [8] (i.e., changing its shape, temperature gradient [12], etc) removing or adding material [17] (i.e., ant-inspired chemical pheromone trails [6,12,15,16,34], etc), anything to leave a trace of an individual’s event for communicating with other individuals at a later time (an indirect interaction). For instance, termites create terrain configurations that stimulate other termites who encounter it to add more building material [17]. Interactions continually change along with the neighbors encountered (i.e., network links are continually formed and broken) [9]. By environmentally encoding events in this way, communication signals can be temporally frozen at that location to eventually influence other robots. Stigmergy cleverly converts temporal data into spatial information (as the time delay extends the spatial range of the link connecting mobile nodes) and therefore also has the potential to compress spatial information into temporal data [31]. Implicit interactions (indirect nodal links) allow for a more complex network structure, giving the swarm (dynamic network) greater flexibility and greater potential to compute more sophisticated emergent behaviors [8].

# NetLogos inbuilt agents (referred to as turtles) were used to represent the robots of the swarm. The robotic swarm is populated with robots which are randomly positioned (random-xcor...) in the environment (an amount specified by swarm-size-a user-defined variable). The triangular shape was used to indicate the orientation of the robots.

to setup

create-robots swarm-size [set size 2 setxy random-xcor randomycor]

# The robots operate within an unbound 2D world which wraps around vertically and horizontally. The obstacles and goals are also modelled using turtles; however, to differentiate them from robots, they are given a different breed (breed [obstacles...]) and, unlike robots, remain static (although by modelling them as turtles, there is potential in future testing for the obstacles to move around; creating a dynamic environment).

Breed [robots robot]

Breed [obstacles obstacle]

Breed [goals goal].

Modelling the robotic swarm across time

When the temporal element is added to the spatial analysis (i.e., analyzing the development of the swarms behavior over time) an extra dimension is required to represent this change over time. In the case of 1D CAs, the space-time diagram is a 2D surface. However, in the case of 2D CAs, the space-time diagram is a 3D surface [24]. Since a particle swarm representation or a network representation are both 2D representations, the added dimension required for the temporal element of the spatio-temporal analysis will have to be represented via a 3D representation.

Robotic swarm behavioral design

Each robot runs on a simple set of rules which govern how the individual reacts to localized changes or events [32]; in other words, how to interact with nearby robots and the environment. In swarm robotics, there are still no formal or precise ways to design individual level behaviors that produce the desired collective behavior [12]. In general, however, emergent behavior in swarm robotics can be modelled from two angles: the microscopic level (a bottom-up, behavior-based approach) and the macroscopic level (a top-down, evolutionary based approach) [12].

The Behavior-based approach: The designer will seek out that the simplest, nonlinear behavior that produces the desired complex global behavior [34] using their personal intuition [12], trial and error and continual tweaking. The bottom-up approach (a.k.a. exploratory based method [56]) is somewhat similar to the scientific method [7]. The skill of identifying the root causes that lead to desired global behaviors is still largely dependent on the designer’s intuition; however, there are some approaches that try to determine these root causes in a principled way [8]. The Voronoi rule and the Virtual forces rule and are two example swarm behaviors designed in this way.

#THE VORONOI RULE

# Initially, a number of obstacles (displayed as circles) are randomly positioned around the environment.

setup-obstacles [

Create-obstacles no-of-obstacles [set shape "circle" set size 2 setxy abs (random-xcor) random-ycor]].

# The robots (displayed as triangles) are also positioned randomly around the environment.

to setup-swarm

create-robots swarm-size [set color grey set xy abs (random-xcor) (random-ycor)].

#Each robot runs the same rule (the rule consists of the robot measuring the distance to its closest obstacle).

to-report nearby-obstacles

report obstacles with-min [precision (distance myself) 1].

# If there is only a single, closest obstacle, the robot will move slightly forward toward it (fd 0.04) after which it turns at a random angle.

to swarm-rule

ask-concurrent robots [

if count nearby-obstacles=1 [

if( xcor >1) [fd 0.04 set color [color] of one-of nearby-obstacles] ]

rt 0.5-random-float 1

]

# Robots will continue to execute this simple rule until they end up at a location where there will be more than one closest obstacle (i.e., two or more obstacles which have the same distance from the robot). At this point the robot stops moving. This behavior causes the swarm to equally segregate obstacles by self-organizing into boundaries between all obstacles (creating a pattern resembling a voronoi map).

#THE VIRTUAL-FORCES RULE

#On each iteration, robots calculate all the surrounding virtual forces coming from neighboring robots as well as the repulsive virtual forces from walls and other obstacles and attractive virtual forces from goals and chemical heat trails left in the environment by other robots.

to update-vfmodel

robot-forces

obstacle-forces

goal-forces

environmental-forces

#To calculate the virtual forces coming from other robots, a robot will query all neighboring robots, goals and obstacles within a certain radius from itself.

#The robots local communication is limited to the maximum range of its sensors (a user-defined variable). Each neighboring obstacle will have a negative force to repulse the robot (set delta 1.0), whereas goals will have a positive force to attract them (set delta 1.0).

#Neighboring robots have a positive (attractive) virtual force by default to encourage the swarm to cohere and stick together. However, neighboring robots closer than a certain radius (known as the robots personal-bubble) have a negative (repulsive) force to avoid collisions.

to robot forces

Ask other robots in-radius sensor-range [

set delta 1.0 if (D<personal bubble)

[set delta 1.0]

#The magnitude of the virtual force (F) is calculated as the squared inverse of the neighboring robots distance (F=1/D^2) so that the closer the robot is, the stronger the virtual force gets. This was found to provide more stable swarm behavior than a linear inverse relationship (F = 1 / D).

let F (rbt-strength/(D*D))

#The virtual force is then used to update the robots velocity which is used to update the robots position. This process is applied to all robots and repeated at each time step.

Turtles-own [Fx Fy delta]

ask myself [set Fx (Fx+(cos (Th+delta*heading)*F))

set Fy (Fy+(sin(Th+delta*heading)*F))]

To update-motion

facexy (xcor+Fx) (ycor+Fy)

setxy (xcor+Fx) (ycor+Fy).

#When first deployed, the robots move chaotically and react to the virtual forces they experience locally. The swarm is very dynamic at this stage and able to easily flow around obstacles (its state is analogous to a fluid). Eventually, all the virtual forces on each robot become balanced and when the net force on each robot is zero and the swarm is in equilibrium, the robots no longer move. As if crystallizing, the swarm comes to a rest in formations resembling straight lines (analogous to a solid polymer) or regular lattices (analogous to a solid crystal).

The evolutionary-based approach: One of the main problems with designing robotic rules manually is that it often taking a long time to refine rules before yielding any successful results. Automatic design methods (like Genetic Algorithms) can be considered top-down methods because, in theory, the process is driven by the global goal [12] i.e., the desired holistic-characteristics of the entire swarm [12]. The perspective is shifted away from the individual to the higher-level of the collective [12]. Unlike bottom-up approaches (i.e., Behavior based approaches) which focus on designing at the level of the local rule, incrementally refining it based on careful observations of the global effects they produce when thoroughly tested [12], top-down approaches (a.k.a. Phenomena based approaches [56]) focus only on the big picture, designing at the global level, some desired model of swarm behavior, which is then used to guide and direct a quick, automatic search through a sea of potential rules until some are found which can produce the desired global properties.

Genetic algorithms: A Genetic Algorithm comprises of an initial set of candidate solutions encoded into genomes. At each generation the fitness of the solutions are determined. Genomes are then paired off to reproduce via crossover and mutation (the fitter candidates being given higher preference in mating to drive the evolutionary process toward the goal). The offspring, along with a small percentage of the fittest parents from the previous generation, survive onto the next generation while the remaining dies off. The process is iterated until a generation evolves to meet an acceptable level of fitness.

Fine-Tuning the hyper-parameters of a Genetic algorithm: The genetic algorithm can find a desired solution fairly efficiently if suitable representational methods, selection pressures (fitness function) and hyper parameters (e.g., population size, probability of mutation, etc) are fine-tuned. The automated search process cannot be applied blindly and effortlessly [23]. Designing the artificially intelligent algorithm well and fine-tuning its parameters determines how quickly, efficiently and optimally the solutions are evolved. It is not sufficient to start somewhere completely random and hope to evolve a solution somewhere in phase space [30]. Factors to carefully consider when designing a Genetic Algorithm include: (a) Representational methods (Genotype and Phenotype), (b) Selection Pressures (Fitness functions), (c) Exploitation (Crossover) and Exploration (Mutation) of the search space, (d) Memory to allow the influence of past solutions (inheritance).

Representational methods (Genotype Phenotype) A chromosome or genotype refers to the encoded solution which the genetic algorithm can search and evolve [8]. The phenotype refers to the coding method which dictates how the chosen representation (directly or indirectly) maps to the real solution (i.e., the rule set used by the robot) [57]. It is used by the genetic algorithm during its search to translate encoded solutions into their corresponding behaviors so that evolving solutions can be evaluated (i.e., to know if the solutions are getting closer to the desired emergent behavior). A common example of a representational method is the bit string [24] or binary string [31] (the candidate solution encoded in binary-a single line of 0s and 1s), the length of which may vary depending on the size of the solution being represented (e.g., 8 bits can represent a number in the range −10 to +10. 128 bits can represent a single transition rule for a 1D binary state CA of radius 3 [31]).

Hexadecimal may be used instead of binary to allow for shorter string lengths [57]. Alternatively, the encoding can be completely specified by the designer, such that the genotype may consist of different letters of the alphabet (e.g., A, B, C, D) [57]. The template representation [31] is an example of a user-defined representation to suit the solution being encoded. A unique feature is the inclusion of a special character to represent any option (i.e., if the string is binary, then would mean 0 or 1). This is a makes the representational method far more expressive by cleverly allowing for generalizations (e.g., the string [0,,] could mean any of the following: [0,0,0], [0,0,1], [0,1,0] or [0,1,1]). The template representation was found to produce superior performance to the bit string traditionally used for representing Cellular Automata [31].

Selection pressures (Fitness Functions) Along with selecting a good representation, selecting an appropriate fitness function (the evaluation method to calculate how a candidate solution ranks against the others [24]) greatly influences the success of the evolutionary process [57]. An example fitness function explored was based on snap (the 4^th order derivative of position, i.e., the rate of change of acceleration). Snap is often used to measure how much an object is shaking (the higher the snap, the higher its shakiness). Therefore, if robots have lower snaps, smoother swarm behaviors emerge, whereas higher snaps produce incoherent, erratic swarm behaviors since each robot is changing their motion very suddenly and violently. Exploitation (Crossover) and Exploration (Mutation) of the search space The initial generation consists of randomly sampled solutions which the genetic algorithm modifies (using specific evolutionary search techniques such as crossover and mutation [24,57]) as a way of exploiting the current best solutions to intelligently navigate through the search space [24].

#CROSSOVER

#Once all individuals in the population have been evaluated (and ranked), their fitnesses are used as a basis for selection [57]. Crossover involves a pair of (parent) candidate solutions exchanging genetic material (i.e., mating/sexually reproducing) [57] by stitching together pieces of their chromosomes to form a new, unique (offspring [41]) candidate solution.

#A random number between 1 and the maximum length of the genome (L) determines the location to split each parent genome (splitpoint).

let split-point random L

#For every two parents who reproduce, both possible combinations were explored. Thus two children are always produced (e.g., A-A & B-B A-B & B-A).

to new-child [split-point strategy_dad strategy_mum] hatch 1

[set strategy crossover split-point

strategy_dad strategy_mum

set th heading

set v 0

set a 0

set fitness 1000

set color one-of base-colors

]

to-report crossover [split-point strat_1 strat_2]

set strat_1 sublist strat_1 0 split-point

set strat_2 sublist strat_2 split-point

(length strat_2)

let strat_mix sentence strat_1 strat_2 report strat_mix

#Occasionally they will combine the best genes of both parents [30] and produce fitter candidate solutions (thus driving the evolution).

#Mutation

#Repeated reproduction with similar genetic information increases genetic homogeneity [47] which can lead to the algorithm getting stuck at a local minima in the search space [30]. To avoid this and encorage exploration of the entire search space, a random element is introduced to add some variety back into the gene pool. Parts of the offsprings chromosome are randomly changed to a different value in a process known as mutation [24].

to respawn-and-mutate

let strategy_dad strategy

hatch 1 [

setxy random-xcor random-ycor

set heading random 360

set strategy mutate strategy_dad

set th heading

set v 0

set a 0

set fitness 1000

]

die

#One of the elements in the genome is picked at random and replaced (replace-item(random...) with a random, new value (one-of command).

to-report mutate [strat]

set strat replace-item (random (L - 1))

strat one-of commands

report strat

Memory to allow the influence of past solutions (Inheritance): There remains a small possibility that the offspring will not be as good as their parents. Thus, elitist inheritance allows the fittest candidates from the previous generation to survive on to (be copied into) the next generation along with all the offspring [24,31,57]. Inheritance can also be thought of as a way for the genetic algorithm to remember best candidate solutions searched in the past and thus act like a memory to help improve the efficiency of the search [31] (Figure 6). Using an excessive memory, however, can actually inhibit the evolutionary process and so selecting an appropriate amount of memory is thus important for effective problem solving [31].

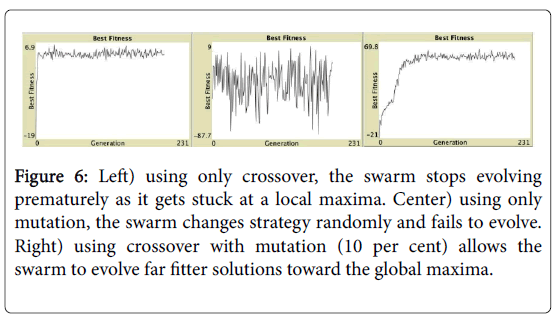
Figure 6: Left) using only crossover, the swarm stops evolving prematurely as it gets stuck at a local maxima. Center) using only mutation, the swarm changes strategy randomly and fails to evolve. Right) using crossover with mutation (10 per cent) allows the swarm to evolve far fitter solutions toward the global maxima.

to elite-replace-inheritance

let number-to-replace round ((1.0 - percentage-elite)*count turtles)

ask min-n-of number-to-replace turtles [ -1 * fitness] [ die]

let best-turtles turtle-set turtles

Analysis

Upon analyzing the spatial interactions of robotic swarms over time, an intricate subsystem of spatio-temporal patterns were revealed (emergent signals used to process, store and communicate information across the decentralized system) embedded within the medium of the system itself. Thus confirming our initial hypothesis that there exist embedded computational mechanics (i.e., the spatio-temporal patterns) which govern the emergent behavior of robotic swarms. This section categorically presents examples of the various types of spatiotemporal patterns discovered, as well as some of their computational mechanics, with some commentaries to explain how each feature is believed to contribute toward the robotic swarms emergent behavior. The various findings are then compared against past research (conducted in Cellular Automata-wherein the theory of spatio-temporal structures and embedded computation was initially developed).

There were four distinct types of spatio-temporal patterns discovered during our analysis (which seem to correspond with the four classes of Cellular Automata): 1. Type I: Static Patterns (corresponding to Class I CAs: Fixed Point Attractors) 2. Type II: Stable Patterns (corresponding to Class II CAs: Periodic Attractors). 3. Type III: Non-Patterns (corresponding to Class III CAs: Chaotic Attractors). 4. Type IV: Semi-Stable Patterns (corresponding to Class IV CAs: Strange Attractors).

Type I: Static patterns (class 1: fixed-point attractors)

The first type of spatio-temporal pattern is static by nature; it remains unchanged over time (often shown as a straight line on the 3d swarm representation (Figure 7). This is commonly formed when a single robot becomes disconnected from the swarm and, having no external influences to react to nor virtual forces acting on it; it remains in the same position over time. There were also examples of static patterns being formed via pairs of robots (depicted as two parallel straight lines on the 3d swarm). Sometimes they can even form via robot trios, although it seems that static spatio-temporal patterns become rarer to find as the number of robots composing it increases. This may be because the positions for robots that robots settle into require a perfect symmetry to balance each other’s influence (even a slight perturbation is enough to shift a robot out of sync and thus cause the others to become unbalanced).

Figure 7: A robotic swarm exhibiting Type I Spatio-Temporal Patterns, visible as static lines over time (left). The robotic swarm is locked in a crystallized lattice, analogous to being in a solid state (right).

Type II: Stable patterns (class 2: periodic attractors)

The second type of spatio-temporal structure is a stable (or cyclical) pattern (repeating the same, stable movements over time (Figures 8 and 9) which corresponds to periodic attractors in CAs. These patterns are most commonly formed from robot pairs caught in a stable dance around one another, reminiscent of binary stars moving back and forth around one another. The exact shape of the pattern produced may vary.

Figure 8: Sometimes less stable patterns collapse into static, type 1 spatio-temporal patterns. This may occur if there are two or more robots affecting one another and their influences balance and cancel each other out, causing them to collapse into a state of equilibrium after an initial chaotic dance.

Figure 9: Two robots (red and purple) form a type II spatiotemporal Pattern shown over time as a cyclical, periodic twirl. The swarm in this state is dynamic yet moves in a repetitive, predictable manner unlike the nearby type IV pattern produced by thee green and blue robots.

Type III: Non-patterns (class 3: chaotic attractors)

The third class of spatio-temporal pattern is when the swarm does not form any pattern at all; the robotic movements and interactions are unstable and extremely random such that no movements are exactly repeated over time (Figure 10). It is in a chaotic state which changes unpredictably. When the swarm is in this state its dynamics resemble a fluid, which is in direct contrast with the solid-like stillness of the first two types of spatio-temporal patterns.

Figure 10: A type III spatio-temporal Pattern, showing a lack of patterns (”chaos”) over time. The swarms are highly dynamic and quickly change shape, similar to a turbulent fluid.

Type IV: Semi-stable patterns (class 4: strange attractors)

The fourth and final type of spatio-temporal pattern discovered is the semi-stable pattern which corresponds to “strange attractors” (Figures 11-13). They are not completely random (like type III) nor completely orderly and repetitive (like types I and II). They balance delicately on the border of stability; between stable and unstable; between order and chaos. This state is one of the most interesting and is also referred to “the edge of chaos” because the swarm can easily drift in and out of being borderline-stable (types I or II) to wildly unstable (type III). To give an analogy in line with the solid and fluid descriptions given for the first three types of patterns, type IV patterns would most closely resemble the turbulent vortex structures that sometimes appear within fluids (and then just as quickly disappear again).

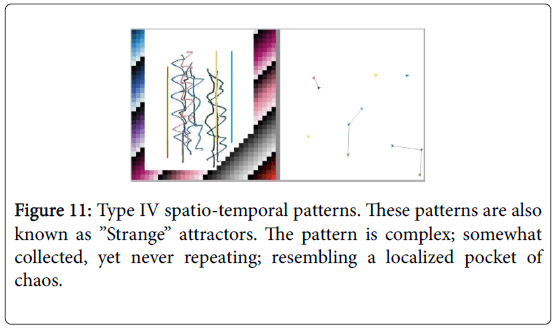
Figure 11: Type IV spatio-temporal patterns. These patterns are also known as ”Strange” attractors. The pattern is complex; somewhat collected, yet never repeating; resembling a localized pocket of chaos.

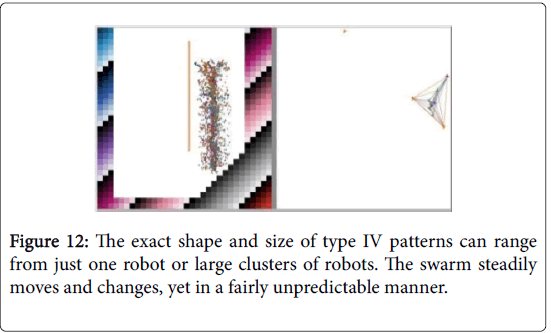
Figure 12: The exact shape and size of type IV patterns can range from just one robot or large clusters of robots. The swarm steadily moves and changes, yet in a fairly unpredictable manner.

Figure 13: A type IV spatio-temporal pattern splitting into two new type I spatio-temporal patterns. This split also causes the information being carried to transform.

Stationary patterns

Solid, stationary spatio-temporal patterns (which resemble a vertical line or pattern) represent robots that remain at or around a particular x-y coordinate. Such patterns give the swarm stability and fix it into a specific formation or shape (which can serve as a memory - assuming information has been encoded into the specific patterns and formation of the swarm). It has been found that pieces of information are represented through the pattern of the spatio-temporal structure (and thus when the pattern changes, so does the information it is representing). Therefore, information can only be stored in the system if it remains unchanged as a type I (fixed-point static) pattern or a type II (periodic stable pattern). Non-patterns (type III) cannot possibly represent information (since they have no recognizable patterns to represent the information), yet they still serve an important computational purpose. Firstly their fluidity gives them the freedom to move across space and time and influence other parts of the swarm, changing nearby spatio-temporal patterns (and the information they represent) in their paths. Secondly, they act as nucleation sites for random seeds form into patterns (i.e., out of the chaos, spatiotemporal patterns may suddenly form or transition from one form to another) (Figure 10).

Dynamic patterns

Diagonal spatio-temporal patterns represent robots slowly moving around the environment while maintaining a shared formation relative to one another. Dynamic patterns serve to transfer information (stored in spatiotemporal patterns and formations) across the swarm, which may then influence a change in other patterns (and their information) through various collision-based computations (i.e., merging, etc) which shall be looked at shortly (Figure 14).

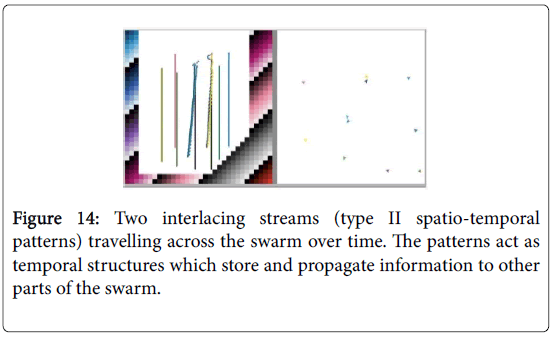
Figure 14:Two interlacing streams (type II spatio-temporal patterns) travelling across the swarm over time. The patterns act as temporal structures which store and propagate information to other parts of the swarm.

Merging splitting patterns

Occasionally, two or more spatio-temporal patterns will collide and merge together to form a new, single pattern. This can be viewed as a collision-based computation (i.e., a computational mechanism which allowed information to be modified in a specific way). Information stored as a single spatio-temporal pattern may also split apart into two or more spatio-temporal patterns (each representing new information) (Figure 15).

Influencing patterns at a distance

Sometimes a spatio-temporal pattern influences a nearby pattern; changing its pattern type while remaining unchanged itself. This type of change can occur if two or more patterns come into direct contact or within close proximity (in range of the robots virtual forces). The patterns seem to conserve momentum as the larger of the two patterns (i.e., the one consisting of more robots) tends to remain unchanged while the smaller pattern is more easily influenced (i.e., changed) (Figure 15).

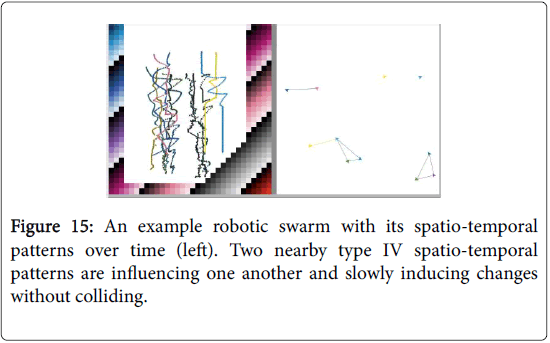
Figure 15:An example robotic swarm with its spatio-temporal patterns over time (left). Two nearby type IV spatio-temporal patterns are influencing one another and slowly inducing changes without colliding.

Decaying patterns

The final type of change occurs when a type III or IV pattern decays into another pattern type without any external influences, either gradually or all of a sudden. This may occur because the type III (chaotic) and type IV (semi-stable) patterns can easily fluctuate due to their innate randomness, unlike more orderly patterns (type I or II). This is also why a type I (static) or type II (stable) pattern never decays into other patterns without an external influence. Decaying is akin to a turbulent vortex structure (with a definite shape) but constantly changes in size and shape over time (sometimes even disappearing or reappearing momentarily). The exact time it takes for a pattern to decay varies, although smaller cluster sizes tend to have shorter lifespans than larger clusters, reminiscent of radioactive half-life decay times (Figures 16 and 17).

Figure 16:The red and purple robots form a type II periodically stable spatio-temporal pattern which is slowly decaying as the robots widen apart. The pattern eventually decays into a type IV semi-stable pattern like the blue and green robots to its right.

Figure 17:Two type II stable spatio-temporal patterns can be seen interweaving back and forth over time. They both slowly decay and destabilize into type IV semi-stable patterns.

Assessment

Results which confirm previous research The discovered patterns lend proof to the theory that computational mechanisms govern the intelligent, self-coordinating, emergent behaviors in swarms of simple, reactive robots (similar to how they govern the emergent behavior in Cellular Automata). The majority of our findings were in line with previous research findings related to spatiotemporal patterns (in Cellular Automata), including: There are many different spatiotemporal patterns (i.e., different spatial configurations perpetuating over time) [10,19]. Each pattern represent a separate piece of information encoded into the system [10,19]. The perpetuation of spatio-temporal patterns allow for pieces of information to be stored, like a memory. Data is stored so long as the patterns persist while remaining unchanged [10,19,39]. Moving spatio-temporal patterns (i.e., not those remaining stationary but those which change spatial coordinates over time) transfer pieces of information across the system [10,19,24]. Changing a spatiotemporal pattern corresponds to changing the associated piece of information [10,19]. A number of Stable types of Spatio-Temporal Patterns were identified [10]. Some unstable (semi-stable) spatio-temporal patterns also exist [10] Stable Spatio-Temporal Patterns can change if influenced by an external event (i.e., collisions with other spatio-temporal patterns) [5,10,18,51]. Unstable (Semi-stable) Spatio-Temporal Patterns can spontaneously change pattern or velocity without any external influences [10].

Results not found in previous research, however, some findings did differ, and even contradict, the findings of prior research (conducted into Spatio-Temporal Patterns governing emergent behavior in Cellular Automata) which have provided us with new insights and additional details about the computational mechanisms governing the emergent behavior of robot swarms. These include: Rather than the two pattern types identified (i.e., stable and unstable), our research identified four distinct pattern types; static (fixed-point attractors), stable (periodic-attractors), non-patterns (chaotic attractors) and semi-stable (strange attractors). On top of discovering unstable (semistable) patterns that could spontaneously change without any external influence (decay), our research suggested that the average decay time (half-life) of semi-stable patterns is proportional to the number of robots involved in forming the semi-stable spatio-temporal pattern (i.e., the smaller the pattern, the shorter the half-life).

Our research found that there were far more stable patterns types than unstable (semi-stable) types when the swarm was in the relatively rare solid state. However, when the robot swarm is in its more common fluid state, the chaotic and unstable (semi-stable) pattern types dominate the scene, in direct contrast to the research findings involved with Cellular Automata. As well as spatiotemporal patterns being modified via collisions with other spatio-temporal patterns [10,19], our research showed that spatio-temporal patterns did not require direct collisions to change. Rather, patterns could influence one another at a distance proportional to the range of the robots virtual forces. Our research identified at least seven distinct pattern changes (i.e., potential logic gates), including; merging (two patterns combine to form a single, new pattern), splitting (one pattern becomes two new patterns), absorbing (one pattern disappears into another larger pattern which remains almost completely unchanged), annihilating (patterns dissolve into the chaos of a type III non-pattern), forming (patterns form out of the chaos of a type III nonpattern), overwhelming (the smaller of two patterns change while the larger remains unchanged), decaying (a pattern changes randomly without any external influence).

Our research also seems to suggest that even though chaotic type III non-patterns are unable to represent, store or transfer specific pieces of information, they do contribute to the computational mechanics of the emergent behavior in other ways; namely by keeping the swarm fluid and thus able to change, having an external influence on nearby patterns, and providing a chaotic environment for spatio-temporal patterns to form from or annihilate into. While our research supports the finding that emergent behavior is not possible if the swarm is fixed in a solid state (i.e., composed of purely type I static or type II stable patterns), it does not limit emergent computation to type IV semistable patterns only. Rather, emergent computation is possible in any dynamic, fluid swarm state (i.e., at least partially composed of type III non-patterns or type IV semi-stable patterns), which includes chaotic (type III) spatio-temporal non-patterns, which have previously been considered incapable of emergent computation.

Future Research

The first three sub-aims were successfully accomplished, wherein robotic swarms were designed by hand, evolved by a genetic algorithm and analyzed to uncover (for the first time) the hypothesized computational mechanisms (spatio-temporal patterns) believed to underlie the emergent behavior of robotic swarms. In doing so, we have made significant steps toward our ultimate goal of intrinsically controlling the emergent behavior of robotic swarms. In future, we hope to conduct a more in-depth study of the discovered spatiotemporal patterns (cataloguing each of their characteristics) and their computational dynamics (mapping their interactions and pattern changes) in order to accurately model the swarm’s computational mechanics. Thereafter we hope to conduct an investigation into possible methods of manipulating these individual spatio-temporal patterns (i.e., using external stimuli, modifying the environment, manipulating key robots, their parameters, the initial configurations, noise, communication delay, etc). Using these manipulation methods with our predictive model, we could potentially control the robotic swarm’s emergent behavior via reprogramming its internal spatiotemporal computations.

The fourth sub-aim (“understand the computational mechanics...”) involves studying the spatio-temporal patterns and gathering enough information about them to accurately model the underlying computational mechanics of the swarm’s emergent behavior. This includes carefully cataloguing every spatio-temporal pattern and their characteristic properties (i.e., class/type, shape, velocity, etc.) and mapping out each type of change it undergoes upon interacting with other spatio-temporal patterns (the collision-based logic). The analysis section of this project has already shown sufficient evidence that differing types of spatio-temporal patterns exist. It has also demonstrated some examples of the typical behaviors and interactions noted. However, these findings are too general and qualitative to answer the fourth aim. For this aim, a far deeper analysis is required in order to obtain the details required to model the intrinsic logic of the swarms underlying spatio-temporal patterns.

Aside from being a more systematic and indepth analysis of the spatio-temporal patterns themselves (the fundamental information processing elements), it would include numerous observations being made to map out their computational dynamics [10], mechanics and nonlinear logical operations (spatio-temporal pattern collisions and interactions cause the pattern and thus the information it represents, to change according to a specific, intrinsic logic [10,26]). Therefore, just like an artificial particle physicist [18], we would carefully observe and catalogue each type of pattern and interaction (or collision) in a lookup table that can later be used to support sophisticated particle-based information processing [10]. This approach is known as computational mechanics (or alternatively collision-based computations) and was first developed as the result of the research conducted into intrinsic computations embedded in CA space-time configurations [58,59]. Spatio-temporal dynamics, representing basic logical operators, (is) the foundation of (collision-based) computation [47].

The findings obtained from the fourth aim are also significant in confirming or contradicting previous research findings (including but not limited to): Basic Logical Operators (i.e., Spatio-Temporal Patterns) The total number of static, stable and semi-stable spatiotemporal patterns (the basic logical operators) which exist [10,28,29,47]. The associated velocity (speed and direction) of each spatio-temporal pattern which determines how information is propagated throughout the system [10,19,24] Collision-based Logic Gates (i.e., Interactions/Pattern Changes) Collisions change the spatiotemporal pattern and velocity according to an intrinsic logic specific to that system (e.g., spatiotemporal patterns and always change into spatiotemporal pattern upon collision) [5,10,18,51]. The inputs of the collision-based logic gates are represented by the spatio-temporal patterns present before the interaction [29,47]. The outputs of the collision-based logic gates are represented by the spatio-temporal patterns present after the interaction [29,47]. The Boolean truth values of collision-based logic gates are represented by the presence and absence of the spatio-temporal patterns [28,29]. The different types of collision-based logic gates which can be realized via the interaction and change of spatio-temporal patterns (i.e., not gates, xor gates, diodes, etc.) [29] The total number of collision based logic gates which occur at the sites where spatiotemporal patterns change via various methods (i.e., Merging, Splitting, Absorption, Annihilation, Formation, Overwhelming, Decay, etc) [10,29].

The fifth sub-aim (”predict the swarms emergent behavior...”) involves simulating the swarms emergent behavior and predicting future developments [33] using a model of its underlying computational mechanics (i.e., the spatio-temporal patterns, their dynamics and intrinsic logic) constructed using the mappings, categorizations and details gathered during the fourth aim (e.g., spatiotemporal pattern types, velocities, collision based computational logic, etc) [10]. The predictive accuracy obtained when modelling the computational mechanics of Cellular Automata in this way was as high as 98.5% [51]. The models accuracy can be evaluated by comparing its predictions against the swarm’s actual developments. The task here is to try to get as low an error as reasonably possible, since even small errors in the particle (spatio-temporal pattern) velocities or interactions are compounded over time [10].

Repellents have even been shown to divert propagating spatiotemporal structures by phase-shifting those [29] or splitting them into two independent signals (spatiotemporal structures) [20,29]. The signal-wave (spatiotemporal structure) will split then into two signals, these daughter waves shrink slightly down to stable size and then travel with constant shape and the auxiliary wave will annihilate [29]. By carefully timing and positioning these external stimuli (i.e., chemicals, light, impurities, etc.), we can precisely control waves (spatio-temporal structures) trajectory. E.g., Realize U-turn of a signal (spatio-temporal structure) [29] and thus direct the evolution of the systems emergent behavior [28]. The seventh and final sub-aim (”intrinsically control the swarms emergent behavior by reprogramming its underlying computational mechanics”) involves putting all the pieces together; using the predictive model (developed in the fifth aim) along with the manipulative methods (investigated in the sixth aim), to parallel program the swarms collision-based computations by manipulating it at the level of its spatio-temporal patterns (i.e., injecting, removing, reflecting, attracting or repelling spatio-temporal patterns in order to manipulate the collision-based logical operations).

For example, manipulating the velocity of key spatio-temporal structures can allow for prior planning of desired collisions and avoidance of unwanted collisions, thus manipulating when and how data is changed, and ultimately controlling, or programming, collisionbased computations. Rerouting a spatio-temporal structure (by changing its direction and/or velocity) can be used to delay and better coordinate distributed pieces of information [29]. Trying to control the swarms global behavior any other way (i.e., at the level of the local robot rules), without first understanding its underlying computational mechanisms (i.e., spatio-temporal patterns) and collision-based logic, is limited and unpredictable. For example, the robot rules react only to localized spatial or temporal factors [12] (i.e., inter-robot distances) are known to have a significant impact on the global outcome of the entire swarm (i.e., how the rule reacts to inter-robot distances can directly impact the swarms aggregation [25]).

Many of these factors, if fine-tuned, can completely alter the global behavior of the swarm by being modified ever so slightly and so such values can be used as leverage points (tipping points) to directly control swarm behavior (i.e., cause a phase transitions) [36]. However, such control techniques are few and rudimentary. Furthermore, the specifics of how the global behavior will be affected are very general, and thus trial and error is often required to recognize and fine-tune such influences. This aim (which is also our ultimate goal) assumes that spatio-temporal patterns are the fundamental processors of emergent collision-based computations and ultimately, the driving force behind global emergent phenomena in robot swarms.

Conclusion

This project has successfully uncovered the computational mechanisms (embedded spatio-temporal patterns) hypothesized to govern the intelligent, self-coordinating, group behaviors emerging across swarms of simple, reactive robots without the aid of any central controller or leader nor global communication or global knowledge. It provides proof that the theory of computational mechanics (developed to explain the emergent behavior in cellular automata) explains the emergent behavior in robotic swarms. It also suggests that this theory may potentially explain emergent behaviors in all forms of complex adaptive system (i.e., biological neural networks, ant colony behavior, bee hives, etc.) and may be the key that demystifies emergent phenomena itself.

Most of our findings confirmed prior research into spatiotemporal computations conducted in Cellular Automata and supported their findings (i.e., pieces of information are encoded in the spatio-temporal pattern and transferred across the system when the moves over time pattern. Changing a pattern corresponds to changing the information it represents. Stable spatio-temporal patterns can be changed via collisions while semi-stable patterns can change spontaneously without any external influences). Some findings however, did differ. These findings provided us with additional, unique insights (i.e., the average decay time of semi-stable patterns is proportional to the number of robots it consists of, spatio-temporal patterns need not collide directly and can sometimes influence one another from a distance, pattern changes form the basis of the collision-based logic gates and can occur via patterns merging, splitting, absorbing, annihilating, forming, overwhelming or decaying. Chaotic non-patterns contribute to the computational process by influencing nearby patterns, etc.).

Following our discovery, we believe that the key to understand a robotic swarm’s emergent behavior is by understanding its underlying computational mechanics (spatio-temporal patterns) and collisionbased logic (pattern changes and interactions). Therefore, the next step would be to conduct a careful study into the intricate dynamics of the swarms spatio-temporal patterns; analyzing each individual pattern and its characteristics in detail, as well as mapping out various interactions and pattern changes, so as to create an accurate model which is able to predict future emergent behaviors before they occur in the real robotic swarm. Further investigation into methods of manipulating (i.e., injecting, removing, reflecting, attracting, repelling, etc.) spatio-temporal patterns is also needed, and this may include researching the effects of noise and initial configuration on the development of the swarms computational mechanisms. Thereafter, we could reach our ultimate goal of controlling a robotic swarm’s emergent behavior intrinsically by predicting and influencing its underlying computational mechanics.

Compliance with Ethical Standards

Conflict of interests: Mohammed Terry Jack declares that he has no conflict of interest. Arnab Singh Khuman declares that he has no conflict of interest. Kayode Owa declares that he has no conflict of interest.

Ethical approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent: N/A

Acknowledgment

First and Foremost, I would like to thank God; Nurturing-Lord of the (seen and unseen) Worlds.

There’s no mental or physical strength except with Almighty God; Most High. May your veneration be upon our Grand-Master Muhammad and, his family and his companions and peace. Thereafter I’d like to thank my family; Elsa and Terry Weizemann (my beloved parents), Roohi and Fahtima Zahra (my darling wife and daughter), Jrui and Idris (my dearest brothers), Dr. Sahar, Imran and Faizan Khan (my loving in laws), and all aunties, uncles, cousins, nephews and nieces for their continual love, support and encouragement. To my respected Professors in Artificial Intelligence and Robotics at De Montfort University-Archie Singh and Kay Owa-a very special thank you for your guidance, advice and enthusiasm throughout this project. Im also very grateful to my close friends, Ayman (Ian) Vicente and Sheikh Amienoellah Abderoef, for their invaluable companionship and stimulating discussions during my time in Abu Dhabi. Last but not least, I’d like to thank Santa Fe Institutes Complexity Explorer for their terrific online courses and ground breaking research into Complexity Science, which sparked my interest in the fascinating field and eventually lead to the birth of this project.

REFERENCES

1. Devi NR, Uma V, Praveena TS, and Jyothi MN. Emerging and Challenging Applications In Swarm Robotics. Int J Eng Sci 2013;2:318-321.
2. Sharma YK, Bagla A. Security challenges for swarm robotics. Int J InfoTech Know Manag 2009;2: 45-48.
3. Vassev E, Sterritt R, Rouff C, Hinchey M. Swarm technology at NASA: building resilient systems. IT Professional 2012;14: 36-42.
4. Mitchell M. Is the Universe a Universal Computer?. Science’s Compass. 2002;298:65-68.
5. Hordjik W. An Overview of Computation in Cellular Automata. Phys Comp 1996;96:1-10.
6. Serugendo GDM. Autonomous systems with emergent behavior. 2006;429-443.
7. Broberg A, Andersson N, Branberg A, Holmlund K, Janlert LE, et al. Emergent Interaction Systems-designing for emergence. 2001.
8. Winfield AFT. The Emergence Engineers’ Dilemma: it seems we can evolve emergence, or prove emergent properties, but not both. 2010;1-23.
9. Ohkura K, Yasuda T, Matsumura Y. Analyzing macroscopic behavior in a swarm robotic system based on clustering. SICE Annual Conference2011 Proceedings 2011;356-361.
10. Crutchfield JP, Mitchell M (1995) The evolution of emergent computation. Proceedings of the National Academy of Sciences 1995;92:10742-10746.
11. Stirling T, Roberts J, Zufferey JC, Floreano D (2012) Indoor navigation with a swarm of flying robots. 2012;4641-4647.
12. Brambilla M, Ferrante E, Birattari, M, Dorigo M. Swarm robotics: a review from the swarm engineering perspective. Swarm Intel 2013;7:1-41.
13. Bonabeau E, Theraulaz G, Deneubourg JL, Aron S, Camazine S. Self-organization in social insects. Trends Ecol Evol 1997;12: 188-193.
14. Kramper W, Wanker R, Zimmermann KH. Analysis of swarm behavior using compound eye and neural network control. Open Comput Sci 2012;2: 16-32.
15. Mijalkov M, McDaniel A, Wehr J, Volpe G (2016) Engineering sensorial delay to control phototaxis and emergent collective behaviors. Phys. Rev. X 2012;6: 011008.
16. Payton D, Estkowski R, Howard M. Compound behaviors in pheromone robotics. Robotics and Autonomous Systems 2003;44:229-240.
17. Holland O, Melhuish C. Stigmergy selforganization,and sorting in collective robotics. Artificial life 1999;5 :173-202.
18. Hordji k W. Particles That SFI Bulletin, 2001;16: 17-20.
19. Reynaga R, Amthauer E. Two-dimensional cellular automata of radius one for density classification task. Pattern recognition letters 2003;24:2849-2856.
20. Adamatzky A. Slimeware: engineering devices with slime mold. Artificial life 2013;19:317-330.
21. Dorigo M, Trianni V, Ahin E, Gro R, Labella TH, et al. Evolving self-organizing behaviors for a swarm-bot. Autonomous Robots 2004;17:223-245.
22. Spears WM, Spears DF, Hamann JC, Heil R. Distributed physics-based control of swarms of vehicles. Autonomous Robots 2004;17:137-162.
23. Trianni V, Nolfi S. Engineering the evolution of self-organizing behaviors in swarm robotics: A case study. Artificial life 2011;17:183-202.
24. Morales FJ, Crutchfield JP, Mitchell M. Evolving two-dimensional cellular automata to perform density classification: A report on work in progress. Cellular Automata: Research Towards Industry 1998;3-14.
25. Kelley DH, Ouellette NT. Emergent dynamics of laboratory insect swarms. Scientific reports. 2013.
26. Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences 1982;79:2554-2558.
27. Mabrouk MH, McInnes CR. An Emergent Wall following behavior to Escape Local Minima for Swarms of Agents. IAENG International Journal of Computer Science.2008.
28. Costello DL, Adamatzky A. Experimental implementation of collision-based gates in belousov zhabotinsky medium. Chaos, Solitons and Fractals 2005;25:535-544.
29. Adamatzky A. Collision-based computing in Belousov Zhabotinsky medium. Chaos, Solitons and Fractals 2004;21:1259-1264.
30. Hawick KA, Scogings CJ. Complex emergent behavior from evolutionary spatial animat agents. Adaptation, Learning, and Optimization 2010;139-159.
31. Stone C, Bull L. Evolution of cellular automata with memory: The density classification task. Biosystems 2009;97:108-116.
32. Arvin F, Murray J, Zhang C. Yue S. Colias: An autonomous micro robot for swarm robotic applications. International Journal of Advanced Robotic Systems 2014;11: 113.
33. Givigi SN, Schwartz HM A. A game theoretic approach to swarm robotics. Applied Bionics and Biomechanics 2006;3:131-142.
34. Various Emergent Behavior.2013.
35. Martin A, Helmerson K.Emergence: the remarkable simplicity of complexity.2014.
36. Rand W. Introduction to Agent-Based Modeling (Summer 2018).2016.
37. Johnson G. Mindless Creatures Acting Mindfully.1999.
38. Piccinini, G. Computational Modelling vs Computational Explanation: Is everything a Turing Machine, and does it matter to the philosophy of mind?. Australasian Journal of Philosophy 2017;85: 93-115
39. Crutcheld J Evolving Cellular Automata Group (EvCA) Project.
40. Chatty A, Kallel I, Gaussier P, Alimi AM. Emergent complex behaviors for swarm robotic systems by local rules. 2011 IEEE Workshop on Robotic Intelligence in Informationally Structured Space. 2011;69-76.
41. J. Groff. GOOeFloys (Gooey-floweez:Greater Object Oriented evolving Floys).Available: Last accessed 23rd Aug 2017.
42. Bohm D. Wholeness and the implicate order. Psychology Press 10.2002.
43. Peat FD. Non-locality in Nature and Cognition. Nature, Cognition and System II 1992;297-311.
44. Wolfram S. A new kind of science. Champaign: Wolfram media 2002;5:1-1250.
45. de Oliveira GMB, Siqueira SRC. Parameter characterization of two-dimensional cellular automata rule space. Physica D: Nonlinear Phenomena 2006;217:1-6.
46. Hordjik W. Dynamics, Emergent Computation, and Evolution in Cellular Automata. Dissertation. 1999;1-241.
47. Ventrella JJ. A particle swarm selects for evolution of gliders in non-uniform 2d cellular automata. Artificial Life X: proceedings of the 10th international conference on the simulation and synthesis of living systems 2006;386-392.
48. Das, R., Mitchell, M. and Crutchfield JP. A genetic algorithm discovers particle-based computation in cellular automata. International Conference on Parallel Problem Solving from Nature 1994;344-353.
49. Mitchell M, Crutchfield JP, Hraber PT. Evolving cellular automata to perform computations: Mechanisms and impediments. Physica D: Nonlinear Phenomena 1994;75:361-391.
50. Langton CG. Computation at the edge of chaos: Phase transitions and emergent computation. Physica D 1990;42:12-37.
51. Hordjik W. World Wide Wanderings.2013.
52. Packard, NH. Adaptation toward the edge of chaos in Kelso JAS, Mandell AJ, Shlesinger M.F. Dynamic Patterns in Complex Systems 293301. 1988.
53. Martinez GJ, Seck-Tuoh-Mora JC, Zenil H. Computation and Universality: Class IV versus Class III Cellular Automata. J Cell Autom. 2013;7:393-430.
54. Mitchell M, Crutcheld JP, Hordjik W (1996) Embedded particle computation in evolved cellular automata. Proceedings of the Conference on Physics and Computation. 1996.
55. Adamatzky A. On oscillators in phyllosilicate excitable automata. International Journal of Modern Physics C 2013;24:1350034.
56. Rand W. Introduction to Agent-Based Modeling summer 2018. 2016.
57. Forrest S. Genetic algorithms: Principles of natural selection applied to computation. Science 1993;261:872-878.
58. Crutchfield JP, Hanson JE (1993) Turbulent pattern bases for cellular automata. Physica D: Nonlinear Phenomena 1993;69:279-301.
59. Hanson, JE, Crutchfield JP. The attractor Basin portrait of a cellular automaton. J Stat Phys 1992;66:1415-1462.